题目内容
8.函数$y=\frac{x+2}{{{x^2}+3x+6}}$的最大值为$\frac{1}{3}$.分析 令x+2=t,则x=t-2,(t>0);从而化简$y=\frac{x+2}{{{x^2}+3x+6}}$=$\frac{1}{t+\frac{4}{t}-1}$,利用基本不等式化简可得$\frac{1}{t+\frac{4}{t}-1}$≤$\frac{1}{3}$(当且仅当t=$\frac{4}{t}$,即t=2,x=0时,等号成立);从而得到答案.
解答 解:易知x2+3x+6>0,故只需讨论x+2>0,
令x+2=t,则x=t-2,(t>0);
$y=\frac{x+2}{{{x^2}+3x+6}}$=$\frac{t}{(t-2)^{2}+3(t-2)+6}$=$\frac{t}{{t}^{2}-4t+4+3t}$=$\frac{1}{t+\frac{4}{t}-1}$,
∵t+$\frac{4}{t}$≥4,故t+$\frac{4}{t}$-1≥3,故$\frac{1}{t+\frac{4}{t}-1}$≤$\frac{1}{3}$,
(当且仅当t=$\frac{4}{t}$,即t=2,x=0时,等号成立);
故答案为:$\frac{1}{3}$.
点评 本题考查了换元法的应用及基本不等式的化简与应用.

练习册系列答案
相关题目
19.已知i为虚数单位,若复数z满足z=i•(2015+2016i),则$\overline z$为( )
| A. | 2015+2016i | B. | 2015-2016i | C. | -2016+2015i | D. | -2016-2015i |
16.已知角终边上一α点P(-4,3),求$\frac{cos(\frac{π}{2}+α)sin(-π-α)}{cos(\frac{5π}{2}-α)sin(\frac{9π}{2}-α)}$的值.
20.已知点(a,3)和点(3,a)在直线x-2y=0的两侧,则a的取值范围是( )
| A. | ($\frac{3}{2}$,6) | B. | (-6,$\frac{3}{2}$) | C. | (-∞,-6)∪($\frac{3}{2}$,+∞) | D. | (-∞,$\frac{3}{2}$)∪(6,+∞) |
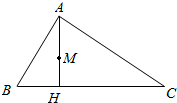 如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.
如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.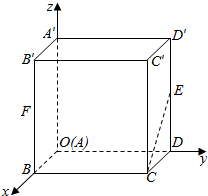 如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.
如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.