题目内容
4.正三棱柱ABC-A1B1C1各棱长均为1,M为CC1的中点,则点B1到截面A1BM的距离为( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 连接B1A交A1B于N,连接AM,则MN为等腰三角形AMB1的中垂线,由此可得结论.
解答  解:连接B1A交A1B于N
解:连接B1A交A1B于N
因为A1ABB1为正方形,所以B1A⊥A1B,且A1N=NB,N为中点
连接AM,则MN为等腰三角形AMB1的中垂线,∴MN⊥AB1,
∴AB1⊥平面A1BM,
∴B1N就是点B1到截面A1BM的距离为$\frac{\sqrt{2}}{2}$
故选:B.
点评 本题考查点到面的距离,考查学生的计算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
14.已知函数f(x)=$\left\{\begin{array}{l}{3^{x+1}}(x≤0)\\{log_2}x(x>0)\end{array}$,则不等式f(x)>3的解集为( )
| A. | (8,+∞) | B. | (-∞,0)∪(8,+∞) | C. | (0,8) | D. | (-∞,0)∪(0,8) |
19.已知i为虚数单位,若复数z满足z=i•(2015+2016i),则$\overline z$为( )
| A. | 2015+2016i | B. | 2015-2016i | C. | -2016+2015i | D. | -2016-2015i |
16.已知角终边上一α点P(-4,3),求$\frac{cos(\frac{π}{2}+α)sin(-π-α)}{cos(\frac{5π}{2}-α)sin(\frac{9π}{2}-α)}$的值.
14.计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量xOy(年入流量:一年内上游来水与库区降水之和(单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系;
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,分别求出安装1台、2台、3台发电机后,水电站所获年总利润的均值,最后确定安装多少台发电机最好?欲使水电站年总利润的均值达到最大,应安装发电机多少台?
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系;
| 年入流量X | 40<X<80 | 80≤X≤120 | X>120 |
| 发电机最多可运行台数 | 1 | 2 | 3 |
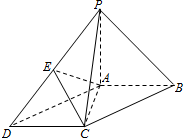 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.