题目内容
若e|sinθ|-ln|cosθ|>e|cosθ|-ln|sinθ|且θ∈(0,π),则θ的取值范围为 .
考点:奇偶性与单调性的综合
专题:计算题,函数的性质及应用
分析:利用e|sinθ|-ln|cosθ|>e|cosθ|-ln|sinθ|,可得|sinθ|>|cosθ|,结合θ∈(0,π),即可求出θ的取值范围.
解答:
解:由题意,θ≠
.
∵e|sinθ|-ln|cosθ|>e|cosθ|-ln|sinθ|,
∴|sinθ|>|cosθ|,
∵θ∈(0,π),
∴θ∈(
,
)∪(
,
).
故答案为:(
,
)∪(
,
).
| π |
| 2 |
∵e|sinθ|-ln|cosθ|>e|cosθ|-ln|sinθ|,
∴|sinθ|>|cosθ|,
∵θ∈(0,π),
∴θ∈(
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
故答案为:(
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
点评:本题考查函数的单调性,考查三角函数知识,考查学生的计算能力,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
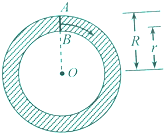 如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×
如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×| R+r |
| 2 |
| R+r |
| 2 |
| A、2πr2d |
| B、2π2r2d |
| C、2πrd2 |
| D、2π2rd2 |
| ∫ | 2 0 |
| A、9 | B、11 | C、14 | D、18 |
 一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积V=
一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积V=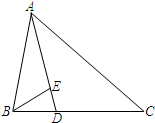 如图,在△ABC中,已知∠BAC=
如图,在△ABC中,已知∠BAC=