Question

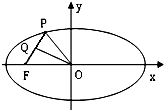如图，P是椭圆

x2

25

+

y2

9

=1上的一点，F是椭圆的左焦点，且

OQ

=

1

2

（

OP

+

OF

），|

OQ

|=4，则|PF|=

 

．

Answer 1

考点：椭圆的简单性质

专题：计算题,平面向量及应用,圆锥曲线的定义、性质与方程

分析：求出椭圆的a，运用椭圆的第一定义，得到|PF|+|PF'|=2a=10，再由向量的中点表示，结合中位线定理，即可得到PF'的长，即可得到PF的长．

解答： 解：椭圆

x2

25

+

y2

9

=1的a=5，
设椭圆的右焦点为F'，则|PF|+|PF'|=2a=10，
由

OQ

=

1

2

（

OP

+

OF

），则Q为PF的中点，
OQ为三角形PFF'的中位线，
则|PF'|=2|OQ|=8，
即有|PF|=10-8=2．
故答案为：2

点评：本题考查椭圆的方程和性质、定义，考查中位线定理，考查向量的中点表示形式，属于中档题．