题目内容
锐角△ABC的面积为3
,a=4,b=3,则角C的大小为( )
| 3 |
| A、75° | B、60° |
| C、45° | D、30° |
考点:正弦定理,余弦定理
专题:解三角形
分析:根据三角形的面积公式,即可得到结论.
解答:
解:∵△ABC的面积为3
,a=4,b=3,
∴S=
absinC=
×4×3sinC=3
,
解得sinC=
,
∵△ABC是锐角三角形,
∴C=60°,
故选:B
| 3 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
解得sinC=
| ||
| 2 |
∵△ABC是锐角三角形,
∴C=60°,
故选:B
点评:本题主要考查三角形面积的应用,根据三角形的面积公式是解决本题的关键.

练习册系列答案
相关题目
在正三棱柱中,AB=AA1=1,P在平面ABC内运动,使得三角形AC1P的面积为
,则动点P的轨迹是( )
| 1 |
| 2 |
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
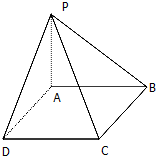 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=