题目内容
已知数列{an}满足a1=
,an=
(n≥2,n∈N*).
(1)证明数列{
+(-1)n}为等比数列,并求数列{an}的通项公式;
(2)设bn=
,求{bn}的前n项和Sn;
(3)设cn=ansin
,数列{cn}的前n项和Tn,求证:对?n∈N*,Tn<
.
| 1 |
| 4 |
| an-1 |
| (-1)nan-1-2 |
(1)证明数列{
| 1 |
| an |
(2)设bn=
| 1 |
| an2 |
(3)设cn=ansin
| (2n-1)π |
| 2 |
| 4 |
| 7 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)把已知的数列递推式取倒数,得到
=(-1)n-
,然后配方得到数列{
+(-1)n}为等比数列,再由等比数列的通项公式求得数列{an}的通项公式;
(2)把(1)中求得的通项公式代入bn=
,然后利用分组求和法结合等比数列的前n项和得答案;
(3)化简sin
=(-1)n,得到cn=
=
,先利用放缩法证明当n≥3时
Tn<
,然后结合T1<T2<T3得答案.
| 1 |
| an |
| 2 |
| an-1 |
| 1 |
| an |
(2)把(1)中求得的通项公式代入bn=
| 1 |
| an2 |
(3)化简sin
| (2n-1)π |
| 2 |
| (-1)n-1 |
| 3•(-2)n-1-(-1)n |
| 1 |
| 3•2n-1+1 |
Tn<
| 4 |
| 7 |
解答:
(1)证明:∵an=
,∴
=(-1)n-
,
∴
+(-1)n=(-2)[
+(-1)n-1],
又∵
+(-1)=3,
∴数列{
+(-1)n}是首项为3,公比为-2的等比数列,
+(-1)n=3•(-2)n-1,即an=
;
(2)解:bn=
=(3•2n-1+1)2=9•4n-1+6•2n-1+1,
Sn=9(40+41+…+4n-1)+6(20+21+…+2n-1)+n
=9•
+6•
+n=Sn=3•4n+6•2n+n-9;
(3)证明:∵sin
=(-1)n,
∴cn=ansin
=
=
,
当n≥3时,Tn=
+
+
+…+
<
+
+
+
+…+
=
+
=
+
[1-(
)n-2]<
+
=
<
,
又∵T1<T2<T3,
∴对?n∈N*,Tn<
.
| an-1 |
| (-1)nan-1-2 |
| 1 |
| an |
| 2 |
| an-1 |
∴
| 1 |
| an |
| 1 |
| an-1 |
又∵
| 1 |
| a1 |
∴数列{
| 1 |
| an |
| 1 |
| an |
| (-1)n-1 |
| 3•2n-1+1 |
(2)解:bn=
| 1 |
| an2 |
Sn=9(40+41+…+4n-1)+6(20+21+…+2n-1)+n
=9•
| 1-4n |
| 1-4 |
| 1-2n |
| 1-2 |
(3)证明:∵sin
| (2n-1)π |
| 2 |
∴cn=ansin
| (2n-1)π |
| 2 |
| (-1)n-1 |
| 3•(-2)n-1-(-1)n |
| 1 |
| 3•2n-1+1 |
当n≥3时,Tn=
| 1 |
| 3+1 |
| 1 |
| 3•2+1 |
| 1 |
| 3•22+1 |
| 1 |
| 3•2n-1+1 |
<
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 3•22 |
| 1 |
| 3•23 |
| 1 |
| 3•2n-1 |
| 11 |
| 28 |
| ||||
1-
|
=
| 11 |
| 28 |
| 1 |
| 6 |
| 1 |
| 2 |
| 11 |
| 28 |
| 1 |
| 6 |
| 47 |
| 84 |
| 4 |
| 7 |
又∵T1<T2<T3,
∴对?n∈N*,Tn<
| 4 |
| 7 |
点评:本题考查了等比关系的确定,考查了等比数列的和,等比数列基本量的求解是等比数列的一类基本问题,解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用,尤其需要注意的是,在使用等比数列的前n项和公式时,应该要分类讨论,有时还应善于运用整体代换的思想简化运算过程,是压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若满足条件C=30°、AB=
、BC=a的△ABC有两个,那么a的取值范围是( )
| 6 |
A、(1,
| ||||
B、(
| ||||
C、(
| ||||
D、(1,2
|
锐角△ABC的面积为3
,a=4,b=3,则角C的大小为( )
| 3 |
| A、75° | B、60° |
| C、45° | D、30° |
已知椭圆
+
=1的长轴在y轴上,且焦距为2,则m等于( )
| x2 |
| 10-m |
| y2 |
| m-4 |
| A、9 | B、8 | C、7.5 | D、7 |
若角α的终边在直线y=2x上,则
的值为( )
| 2sinα-cosα |
| sinα+2cosα |
| A、0 | ||
B、
| ||
| C、1 | ||
D、
|
已知条件p:x2-2ax+a2-1>0,条件q:x>2,且q是p的充分而不必要条件,则a的取值范围是( )
| A、a≥1 | B、a≤1 |
| C、a≥-3 | D、a≤-3 |
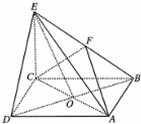 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.