题目内容
5.设函数$f(x)=\frac{1}{x},g(x)=a{x^2}+bx(a,b∈R,a≠0)$,若y=f(x)的图象与y=g(x)图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),有如下命题:①当a<0时,x1+x2<0,y1+y2>0
②当a<0时,x1+x2>0,y1+y2<0
③当a>0时,x1+x2<0,y1+y2<0
④当a>0时,x1+x2>0,y1+y2>0
其中,正确命题的序号是②.
分析 在同一坐标系中分别画出两个函数的图象,利用图象即可得出结论.
解答  解:在同一坐标系中分别画出两个函数的图象,
解:在同一坐标系中分别画出两个函数的图象,
当a<0时,要想满足条件,则有如图,做出点A关于原点的对称点C,则C点坐标为(-x1,-y1),由图象知-x1<x2,-y1>y2,即x1+x2>0,y1+y2<0,
同理当a>0时,则有x1+x2<0,y1+y2>0,
故答案为:②.
点评 本题考查函数的图象,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
13.设F(c,0)是双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点,$P(\frac{a^2}{c},\frac{{\sqrt{2}a}}{2})$为直线上一点,且直线垂直于x轴,垂足为M,若△PMF等腰三角形,则E的离心率为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
20.(文)某学校高一、高二、高三年级的学生人数之比为3:3:m,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,若从高三年级抽取的学生人数为20,则实数m=( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
10.某经销商试销A、B两种商品一个月(30天)的记录如下:
若售出每种商品1件均获利40元,用X,Y表示售出A、B商品的日利润值(单位:元).将频率视为概率.
(1)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(2)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
(1)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(2)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.
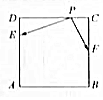 如图,正方形ABCD的边长为8,点E,F分别在边AD,BC上,且AE=3ED,CF=FB,如果对于常数m,在正方形ABC的四条边上有且只有6个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=m成立,那么m的取值范围是(-1,8).
如图,正方形ABCD的边长为8,点E,F分别在边AD,BC上,且AE=3ED,CF=FB,如果对于常数m,在正方形ABC的四条边上有且只有6个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=m成立,那么m的取值范围是(-1,8).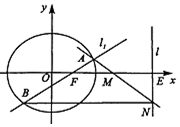 已知椭圆$E:\frac{x^2}{5}+\frac{y^2}{4}=1$的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.
已知椭圆$E:\frac{x^2}{5}+\frac{y^2}{4}=1$的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.