题目内容
2.设三棱锥PABC的顶点P在平面ABC上的射影是H,给出下列命题:①若PA⊥BC,PB⊥AC,则H是△ABC的垂心;
②若PA,PB,PC两两互相垂直,则H是△ABC的垂心;
③若PA=PB=PC,则H是△ABC的外心.
请把正确命题的序号填在横线上:①②③.
分析 根据题意画出图形,然后对应选项一一判定即可.
解答 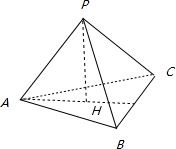 解:①因为PH⊥底面ABC,所以PH⊥BC,又PA⊥BC,所以BC⊥平面PAH,所以AH⊥BC.同理BH⊥AC,可得H是△ABC的垂心,正确.
解:①因为PH⊥底面ABC,所以PH⊥BC,又PA⊥BC,所以BC⊥平面PAH,所以AH⊥BC.同理BH⊥AC,可得H是△ABC的垂心,正确.
②若PA,PB,PC两两互相垂直,所以PA⊥平面PBC,所以PA⊥BC,由此推出AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.
③若PA=PB=PC,由此推出AH=BH=CH,则H是△ABC的外心,正确.
故答案为①②③.
点评 本题考查棱锥的结构特征,考查学生分析问题解决问题的能力,三垂线定理的应用,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.函数f(x)=9x3-ln|x|的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
14.已知集合M={x|-1≤x≤2},N={x|1-3a<x≤2a},若M∩N=M,则实数a的取值范围是( )
| A. | ($\frac{2}{3}$,1) | B. | (1,+∞) | C. | ($\frac{2}{3}$,+∞) | D. | [1,+∞) |
11.已知F是抛物线y2=4x的焦点,过点F且斜率为$\sqrt{3}$的直线交抛物线于A,B两点,则||FA|2-|FB|2|的值为( )
| A. | $\frac{28}{3}$ | B. | $\frac{128}{9}$ | C. | $\frac{128}{8}\sqrt{3}$ | D. | $\frac{28}{3}\sqrt{2}$ |