题目内容
17.已知无穷数列{an},满足an+2=|an+1-an|,n∈N*;(1)若a1=1,a2=2,求数列前10项和;
(2)若a1=1,a2=x,x∈Z,且数列{an}前2017项中有100项是0,求x的可能值;
(3)求证:在数列{an}中,存在k∈N*,使得0≤ak<1.
分析 (1)由条件分别计算前10项,即可得到所求和;
(2)讨论x=1,2,3,…,计算得到数列进入循环,求得数列中0的个数,即可得到所求值;
(3)运用反证法证明,结合条件及无穷数列的概念,即可得证.
解答 解:(1)数列{an},满足an+2=|an+1-an|,n∈N*;a1=1,a2=2,
则a3=1,a4=1,a5=0,a6=1,a7=1,a8=0,a9=a10=1.
∴数列前10项和S10=1+2+6=9.
(2)当x=1时,数列数列{an}的各项为1,1,0,1,1,0,1,1,0,1,1,0…
所以在前2017项中恰好含有672项为0;
当x=2时,数列数列{an}的各项为1,2,1,1,0,1,1,0,1,1,0…
所以在前2017项中恰好含有671项为0;
当x=3时,数列数列{an}的各项为1,3,2,1,1,0,1,1,0,1,1,0…
所以在前2017项中恰好含有671项为0;
当x=4时,数列数列{an}的各项为1,4,3,1,2,1,1,0,1,1,0,…
所以在前2017项中恰好含有670项;
当x=5时,数列数列{an}的各项为1,5,4,1,3,2,1,1,0,1,1,0…
所以在前2017项中恰好含有670项为0;
…
由上面可以得到当x=1144或x=1145时,在前2017项中恰好含有100项为0;
当x=-1141或x=-1140时,在前2017项中恰好含有100项为0;
(3)证明:假设数列{an}中不存在ak(k∈N*),使得0≤ak<1,
则ak<0或ak≥1(k=1,2,3,…).
由无穷数列{an},满足an+2=|an+1-an|,n∈N*,
可得ak≥1,由于无穷数列{an},对于给定的a1,a2,总可以相减后得到0,
故假设不成立.
在数列{an}中,存在k∈N*,使得0≤ak<1.
点评 本题考查了数列求和、分类讨论、反证法的运用,考查了推理能力与计算能力,属于难题.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
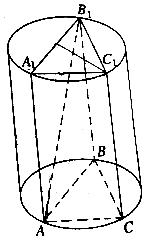 如图,圆柱有一个高6$\sqrt{2}$cm,体积为54$\sqrt{6}$cm3的内接正三棱柱ABC-A1B1C1.
如图,圆柱有一个高6$\sqrt{2}$cm,体积为54$\sqrt{6}$cm3的内接正三棱柱ABC-A1B1C1.求:(1)圆柱的体积;
(2)AC1与正三棱柱的侧面ABB1A1所成角的大小.
| A. | y=-x | B. | y=cosx | C. | y=${x^{\frac{2}{5}}}$ | D. | y=-x2 |
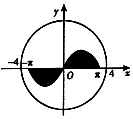 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.