题目内容
11.在锐角△ABC中,A、B、C的对边分别是a,b,c,(a2+c2-b2)tanB=$\frac{4\sqrt{2}}{3}$ac.(1)求sinB的值;
(2)若b=2,S△ABC=$\sqrt{2}$,求a的值.
分析 (1)由已知及余弦定理可得cosBtanB=$\frac{2\sqrt{2}}{3}$,利用同角三角函数基本关系式即可得解sinB的值.
(2)利用三角形面积公式可求ac=3,由sinB可求cosB,由余弦定理可得:a4-6a2+9=0,即可解得a的值.
解答 (本小题满分12分)
解:(1)∵$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$tanB=$\frac{2\sqrt{2}}{3}$,
∴cosBtanB=$\frac{2\sqrt{2}}{3}$,
∴sinB=$\frac{2\sqrt{2}}{3}$.…(6分)
(2)∵S△ABC=$\sqrt{2}$,又S△ABC=$\frac{1}{2}$casinB=$\frac{1}{2}$ac$\frac{2\sqrt{2}}{3}$,
∴ac=3. …(8分)
∵△ABC为锐角三角形且sinB=$\frac{2\sqrt{2}}{3}$,
∴cosB=$\frac{1}{3}$.…(10分)
将b=2,cosB=$\frac{1}{3}$,c=$\frac{3}{a}$代入余弦定理:b2=a2+c2-2accosB,
∴a4-6a2+9=0,
∴a=$\sqrt{3}$.…(12分)
点评 本题主要考查了余弦定理,同角三角函数基本关系式,三角形面积公式,一元二次方程的解法,考查了计算能力和转化思想,属于中档题.

练习册系列答案
相关题目
2.设f(x)为偶函数且在(-∞,0)内是增函数,f(-2)=0,则xf(x)>0的解集为( )
| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(0,2) |
 设全集U=R,集合A={x|(1-2x)(x+3)>0},B={x|$\frac{1}{x}$>1},则图中阴影部分所表示的集合是[$\frac{1}{2}$,1).(用区间表示)
设全集U=R,集合A={x|(1-2x)(x+3)>0},B={x|$\frac{1}{x}$>1},则图中阴影部分所表示的集合是[$\frac{1}{2}$,1).(用区间表示)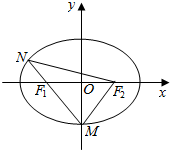 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1、F2分别为椭圆的左、右焦点,M为椭圆的下顶点,直线MF1交椭圆与另一点N.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1、F2分别为椭圆的左、右焦点,M为椭圆的下顶点,直线MF1交椭圆与另一点N.