题目内容
设F1,F2是椭圆
+
=1的两个焦点,P是椭圆上的点且|PF1|:|PF2|=4:3,则△PF1F2的面积为( )
| x2 |
| 24 |
| y2 |
| 49 |
| A、24 | ||
| B、26 | ||
C、22
| ||
D、24
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据椭圆方程,得a=7,椭圆的焦点为F1(-5,0),F2(5,0),由椭圆的定义结合|PF1|:|PF2|=4:3,得|PF1|=8,|PF2|=6,结合勾股定理的逆定理得△PF1F2是以P为直角顶点的直角三角形,由此不难得到△PF1F2的面积.
解答:
解:∵椭圆的方程为
+
=1,
∴a=7,b=2
,c=5.
得椭圆的焦点为F1(-5,0),F2(5,0),
∵|PF1|+|PF2|=2a=14,且|PF1|:|PF2|=4:3,
∴|PF1|=8,|PF2|=6,
可得|PF1|2+|PF2|2=100=|F1F2|2,
因此,△PF1F2是以P为直角顶点的直角三角形,
得△PF1F2的面积S=
|PF1|•|PF2|=24
故选:A.
| x2 |
| 24 |
| y2 |
| 49 |
∴a=7,b=2
| 6 |
得椭圆的焦点为F1(-5,0),F2(5,0),
∵|PF1|+|PF2|=2a=14,且|PF1|:|PF2|=4:3,
∴|PF1|=8,|PF2|=6,
可得|PF1|2+|PF2|2=100=|F1F2|2,
因此,△PF1F2是以P为直角顶点的直角三角形,
得△PF1F2的面积S=
| 1 |
| 2 |
故选:A.
点评:本题给出椭圆的两条焦半径的比值,求焦点三角形的面积,着重考查了椭圆的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设直线y=x+b是曲线y=ex的一条切线,则实数b=( )
| A、-1 | B、0 | C、1 | D、2 |
下列四个条件中,能确定一个平面的是( )
| A、一条直线和一个点 |
| B、空间两条直线 |
| C、空间任意三点 |
| D、两条平行直线 |
函数f(x)=x2•cosx在区间[-
,
]内的图象大致为( )
| π |
| 2 |
| π |
| 2 |
A、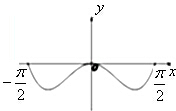 |
B、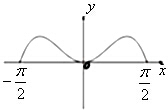 |
C、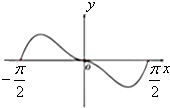 |
D、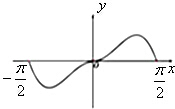 |
互相平行的三条直线,最多可以确定的平面个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知函数f(x)在x0处可导,则
等于( )
| lim |
| △x→0 |
| f(x0-2h)-f(x0) |
| h |
| A、2f′(x0) |
| B、-f′(-x0) |
| C、-f′(x0) |
| D、-2f′(x0) |
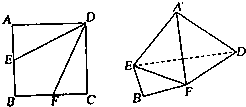 如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△ADE,△CDF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△ADE,△CDF分别沿DE,DF折起,使A,C两点重合于点A′.