题目内容
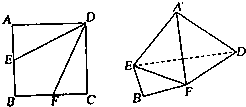 如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△ADE,△CDF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△ADE,△CDF分别沿DE,DF折起,使A,C两点重合于点A′.(Ⅰ)求证:平面A′DE⊥平面A′EF;
(Ⅱ)求三棱锥A′-DEF的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:证明题
分析:(Ⅰ)折叠前后不变的是,A′D⊥A′E,A′D⊥A′F,得到A′D⊥平面A′EF,从而证明平面A′DE⊥平面A′EF;
(Ⅱ)将求三棱锥A′-DEF的体积转化成求三棱锥D-A′EF的体积,再进一步代入计算.
(Ⅱ)将求三棱锥A′-DEF的体积转化成求三棱锥D-A′EF的体积,再进一步代入计算.
解答:
解:(Ⅰ)折叠前,AD⊥AE,CD⊥CF,
折叠后,A′D⊥A′E,A′D⊥A′F,
又∵A′E∩A′F=A′,
∴A′D⊥平面A′EF,
∵A′D?平面A′DE,
∴平面A′DE⊥平面A′EF.
(Ⅱ)∵E,F分别是AB,BC的中点,
∴AE=BE=BF=1,EF=
,
折叠后,A′E=A′F=1,
∴A′E2+A′F2=EF2,∴A′E⊥A′F.
∴S△A′EF=
A′E×A′F=
×1×1=
,
由(Ⅰ),知A′D⊥平面A′EF,
∴VA′-DEF=VD-A′EF=
S△A′EF•A′D=
×
×2=
.
折叠后,A′D⊥A′E,A′D⊥A′F,
又∵A′E∩A′F=A′,
∴A′D⊥平面A′EF,
∵A′D?平面A′DE,
∴平面A′DE⊥平面A′EF.
(Ⅱ)∵E,F分别是AB,BC的中点,
∴AE=BE=BF=1,EF=
| 2 |
折叠后,A′E=A′F=1,
∴A′E2+A′F2=EF2,∴A′E⊥A′F.
∴S△A′EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由(Ⅰ),知A′D⊥平面A′EF,
∴VA′-DEF=VD-A′EF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:在几何体的体积求解过程中,等体积法是经常用到的方法之一,除此之外,还有公式、割补法等常用方法.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
设F1,F2是椭圆
+
=1的两个焦点,P是椭圆上的点且|PF1|:|PF2|=4:3,则△PF1F2的面积为( )
| x2 |
| 24 |
| y2 |
| 49 |
| A、24 | ||
| B、26 | ||
C、22
| ||
D、24
|
用反证法证明命题:“若实系数一元二次方程ax2+bx+c=0(a≠0)有实数根,那么b2-4ac≥0”时,下列假设正确的是( )
| A、假设b2-4ac≤0 |
| B、假设b2-4ac<0 |
| C、假设b2-4ac≥0 |
| D、假设b2-4ac>0 |
 在工商管理学中,MRP指的是物质需要计划,基本MRP的体系结构如图所示.从图中能看出影响基本MRP的主要因素有( )个.
在工商管理学中,MRP指的是物质需要计划,基本MRP的体系结构如图所示.从图中能看出影响基本MRP的主要因素有( )个.