题目内容

函数f（x）=x2•cosx在区间[-
π
2
，
π
2
]内的图象大致为（　　）
A、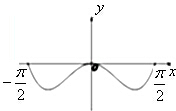
B、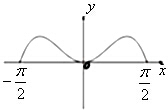
C、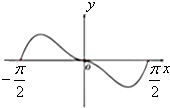
D、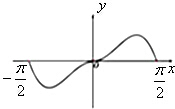
考点：函数的图象
专题：函数的性质及应用
分析：根据函数f（x）=x2cosx是偶函数，且函数在[-
π
2
，
π
2
]内的函数值为正实数，从而得出结论．
解答： 解：由于函数f（x）=x2cosx是偶函数，
故它的图象关于y轴对称，且当x∈[-
π
2
，
π
2
]时，函数值为正实数，
故选B．
点评：本题主要考查偶函数的图象和性质，余弦函数在∈[-
π
2
，
π
2
]的值域，属于基础题．
练习册系列答案
相关题目
若α、β为锐角，且cosα=
1
10
，sinβ=
2
5
，则α+β=
 
．
已知sinα是方程5x2-7x-6=0的根，且α是第三象限角，则
sin(-α-
3π
2
)cos(
3π
2
-α)tan2(π-α)
cos(
π
2
-α)sin(
π
2
+α)
=（　　）
A、
9
16
B、-
9
16
C、
3
4
D、-
3
4
a=3
b=4
a=b
b=a
PRINT  a，b
END
以上程序输出的结果是（　　）
A、3，4B、4，4
C、3，3D、4，3
设函数f（x）=ex-ax，若f′（0）=2，则a的值为（　　）
A、-1B、0C、1D、3
设F1，F2是椭圆
x2
24
+
y2
49
=1的两个焦点，P是椭圆上的点且|PF1|：|PF2|=4：3，则△PF1F2的面积为（　　）
A、24
B、26
C、22
2
D、24
2
对于三次函数f（x）=ax3+bx2+cx+d（a≠0），定义f″（x）是y=f（x）的导函数y=f′（x）的导函数，若方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”，可以证明，任何三次函数都有“拐点”，任何三次函数都有对称中心，且“拐点”就是对称中心，请你根据这一结论判断下列命题：
①任意三次函数f（x）=ax3+bx2+cx+d（a≠0）都关于点（-
b
3a
，f（-
b
3a
））对称：
②存在三次函数有两个及两个以上的对称中心；
③存在三次函数f（x）=ax3+bx2+cx+d（a≠0），若f′（x）=0有实数解x0，则点（x0，f（x0））为函数y=f（x）的对称中心；
④若函数g（x）=
1
3
x3-
1
2
x2-
5
12
，则：g（
1
2014
）+g（
2
2014
）+g（
3
2014
）+…+g（
2013
2014
）=-1006.5
其中所有正确结论的序号是（　　）
A、①②③B、①②④
C、①③④D、②③④
某地区试行高考自主招生考试改革：在高中三学年中举行5次统一测试，学生如果通过其中2次测试即可获得足够学分升上大学继续学习，不用参加其余的测试，而每个学生最多也只能参加5次测试．假设某学生每次通过测试的概率都是
1
3
，每次测试通过与否相互独立．规定：若前4次都没有通过测试，则第5次不能参加测试．
（1）求该学生考上大学的概率；
（2）求该生参加考试次数X的分布列与期望．
化简：
cos(π+α)
cosα[cos(π-α)-1]
+
cos(α-2π)
[sin(α-
3π
2
)cos(α-π)-sin(
3π
2
+α)]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网