题目内容
P为圆C1:x2+y2=9上任意一点,Q为圆C2:x2+y2=25上任意一点,PQ中点组成的区域为M,在C2内部任取一点,则该点落在区域M上的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:根据几何概型的概率公式,求出相应的面积即可得到结论.
法1:根据中点代入法,求出满足条件轨迹方程,即可求相应的面积,
法2:利用三角换元法,求出满足条件轨迹方程,即可求相应的面积.
法1:根据中点代入法,求出满足条件轨迹方程,即可求相应的面积,
法2:利用三角换元法,求出满足条件轨迹方程,即可求相应的面积.
解答:
解:【法1】设Q(x0,y0),中点M(x,y),则P(2x-x0,2y-y0)代入x2+y2=9,
得(2x-x0)2+(2y-y0)2=9,
化简得:(x-
)2+(y-
)2=
,
又x02+y02=25表示以原点为圆心半径为5的圆,
故易知M轨迹是在以(
,
)为圆心,
以
为半径的圆绕原点一周所形成的图形,
即在以原点为圆心,宽度为3的圆环带上,
即应有x2+y2=r2(1≤r≤4),
那么在C2内部任取一点落在M内的概率为
=
=
,
故选B.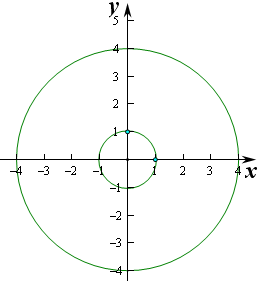
【法2】设P(3cosθ,3sinθ),Q(5cosα,5sinα),M(x,y),
则2x=3cosθ+5cosα,①
2y=3sinθ+5sinα,②,
①2+②2得:x2+y2=
+
cos(θ-α)=r2,
所以M的轨迹是以原点为圆心,
以r,(1≤r≤4),为半径的圆环,
那么在C2内部任取一点落在M内的概率为
=
=
,
故选B.
得(2x-x0)2+(2y-y0)2=9,
化简得:(x-
| x0 |
| 2 |
| y0 |
| 2 |
| 9 |
| 4 |
又x02+y02=25表示以原点为圆心半径为5的圆,
故易知M轨迹是在以(
| x0 |
| 2 |
| y0 |
| 2 |
以
| 3 |
| 2 |
即在以原点为圆心,宽度为3的圆环带上,
即应有x2+y2=r2(1≤r≤4),
那么在C2内部任取一点落在M内的概率为
| 16π-π |
| 25π |
| 15 |
| 25 |
| 3 |
| 5 |
故选B.

【法2】设P(3cosθ,3sinθ),Q(5cosα,5sinα),M(x,y),
则2x=3cosθ+5cosα,①
2y=3sinθ+5sinα,②,
①2+②2得:x2+y2=
| 17 |
| 2 |
| 15 |
| 2 |
所以M的轨迹是以原点为圆心,
以r,(1≤r≤4),为半径的圆环,
那么在C2内部任取一点落在M内的概率为
| 16π-π |
| 25π |
| 15 |
| 25 |
| 3 |
| 5 |
故选B.
点评:本题主要考查几何概型的概率计算,根据条件求出相应的区域及其面积是解决本题的关键.

练习册系列答案
相关题目
设集合A={0,1,2,4,5,7},集合B={1,3,6,8,9},集合C={3,7,9},则集合(A∩B)∪C等于( )
| A、{3,7,9} |
| B、{3,6,7,9} |
| C、{1,3,7,9} |
| D、{0,1,2,6,9} |
复数(1+2i)2(其中i为虚数单位)的虚部为( )
| A、4i | B、-4i | C、4 | D、-4 |
幂函数f(x)的图象过点(4,2),那么f(8)的值为( )
A、2
| ||
B、2
| ||
| C、64 | ||
D、
|
已知函数f(x)=
的定义域为R,试求实数m的取值范围( )
| 1 |
| 22x+m•2x+1 |
| A、(-2,2) |
| B、(-∞,-2)∪(2,+∞) |
| C、(0,2) |
| D、(-2,+∞) |
已知向量
=(1,cosα),
=(2,1)且
∥
,则锐角α的大小为( )
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|x<3},B={x|log2x<2},则A∩B=( )
| A、(-1,3) |
| B、(0,4) |
| C、(0,3) |
| D、(-1,4) |