题目内容
20．如图是某几何体的三视图，则该几何体的体积为（ ）
| A． | 6 | B． | 9 | C． | 12 | D． | 18 |
分析 根据几何体的三视图知该几何体是长方体和三棱柱的组合体，
结合图中数据求出它的体积即可．
解答 解：根据几何体的三视图知，
该几何体是上部为长方体，下部为三棱柱的组合体，
画出几何体的直观图如图所示，
根据图中数据，计算其体积为
V组合体=V三棱柱+V长方体
=$\frac{1}{2}×4×4×1+2×2×1=12$．
故选：C．
点评 本题考查了空间几何体三视图的应用问题，也考查了空间想象能力和体积公式的应用问题，是基础题．
练习册系列答案
相关题目
10．
就某地居民的月收入调查了20000人，并根据所得数据画出了样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500））．根据频率分布直方图可求得样本数据的中位数是（ ）
就某地居民的月收入调查了20000人，并根据所得数据画出了样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500））．根据频率分布直方图可求得样本数据的中位数是（ ）| A． | 2250 | B． | 2400 | C． | 2500 | D． | 10000 |
11．已知变量x，y满足约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ 3x-y+1≥0\end{array}\right.$，则目标函数z=4x+y-2的最大值为（ ）
| A． | 1 | B． | 2 | C． | 6 | D． | 4 |
8．已知非零向量$\overrightarrow a$，$\overrightarrow b$满足$|{\overrightarrow b}|=2|{\overrightarrow a}|$，且$\overrightarrow a$与$\overrightarrow b$的夹角为60°，则“m=1”是“$（\overrightarrow a-m\overrightarrow b）⊥\overrightarrow a$”的（ ）
| A． | 充分不必要条件 | B． | 充要条件 | ||
| C． | 必要不充分条件 | D． | 既不充分也不必要条件 |
15．若$sinθcosθ=\frac{1}{2}$，则$tanθ-\frac{cosθ}{sinθ}$的值是（ ）
| A． | -2 | B． | 0 | C． | ±2 | D． | $\frac{1}{2}$ |
10．执行如图所示的程序框图，若输出S的值为0.99，则判断框内可填入的条件是（ ）
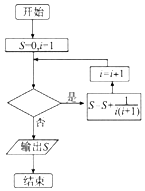
| A． | i＜100 | B． | i≤100 | C． | i＜99 | D． | i≤98 |