题目内容
6．
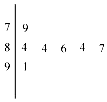某学校举行的演讲比赛有七位评委，如图是评委们为某选手给出分数的茎叶图，根据规则去掉一个最高分和一个最低分．则此所剩数据的平均数和方差分别为（ ）| A． | 84，4.84 | B． | 84，1.6 | C． | 85，4 | D． | 85，1.6 |
分析 所剩数据为84，84，86，84，87，由此求出所剩数据平均数，从而能求出方差．
解答 解：评委们为某选手给出分数的茎叶图，根据规则去掉一个最高分和一个最低分，
所剩数据为84，84，86，84，87，
∴所剩数据平均数为：
$\overline{x}$=$\frac{1}{5}$（84+84+86+84+87）=85，
方差为：S2=$\frac{1}{5}$[（84-85）2+（84-85）2+（86-85）2+（84-85）2+（87-85）2]=1.6．
故选：D．
点评 本题考查平均数、方差的求法，是基础题，解题时要认真审题，注意平均数、方差、茎叶图的性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．全称命题“?x∈R，x2+5x=4”的否定是（ ）
| A． | $?{x_0}∈R，{x_0}^2+5{x_0}=4$ | B． | ?x∈R，x2+5x≠4 | ||
| C． | $?{x_0}∈R，{x_0}^2+5{x_0}≠4$ | D． | 以上都不正确 |
17．定义在R上的函数y=f（x）满足：f（x）+f′（x）＞1，f（0）=2017，则不等式exf（x）-ex＞2016（其中e为自然对数的底数）的解集为（ ）
| A． | （2016，+∞） | B． | （-∞，0）∪（2016，+∞） | C． | （-∞，0）∪（0，+∞） | D． | （0，+∞） |
11．已知变量x，y满足约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ 3x-y+1≥0\end{array}\right.$，则目标函数z=4x+y-2的最大值为（ ）
| A． | 1 | B． | 2 | C． | 6 | D． | 4 |
18．已知点（x，y）满足不等式组$\left\{\begin{array}{l}x-y+3≥0\\ 2x-y-1≤0\\ 3x+2y-6≥0\end{array}\right.$，则$z=\frac{y}{x+1}$的最小值为（ ）
| A． | 3 | B． | $\frac{7}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{7}{5}$ |
15．若$sinθcosθ=\frac{1}{2}$，则$tanθ-\frac{cosθ}{sinθ}$的值是（ ）
| A． | -2 | B． | 0 | C． | ±2 | D． | $\frac{1}{2}$ |