题目内容
7.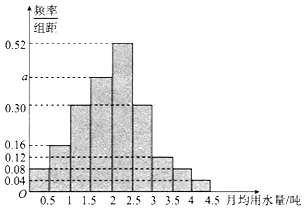 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;
(2)若该市有110万居民,估计全市居民中月均用水量不低于3吨的人数,请说明理由;
(3)估计居民月均用水量的中位数(精确到0.01)
分析 (1)由各组频率和为1,列出方程求出a的值;
(2)由题意计算不低于3吨的频率与频数即可;
(3)利用中位数两边的频率相等,列出方程求出中位数的值.
解答 解:(1)由概率统计相关知识,各组频率之和的值为1,
得0.5×(0.08+0.16+0.3+a+0.52+0.3+0.12+0.08+0.04)=1,
解得a=0.4;
(2)由题中统计图可得,不低于3吨的人数所占比例为
0.5×(0.12+0.08+0.04)=12%,
∴全市月均用水量不低于3吨的人数为
110×0.12=13.2(万);
(3)设中位数为x,则有
0.5×(0.08+0.16+0.3+0.4)+0.52×(x-2)=0.5,
解得x≈2.06,
估计中位数是2.06.
点评 本题考查了频率分布直方图的应用问题,也考查了中位数的计算问题,是基础题目.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
17.定义在R上的函数y=f(x)满足:f(x)+f′(x)>1,f(0)=2017,则不等式exf(x)-ex>2016(其中e为自然对数的底数)的解集为( )
| A. | (2016,+∞) | B. | (-∞,0)∪(2016,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (0,+∞) |
18.已知点(x,y)满足不等式组$\left\{\begin{array}{l}x-y+3≥0\\ 2x-y-1≤0\\ 3x+2y-6≥0\end{array}\right.$,则$z=\frac{y}{x+1}$的最小值为( )
| A. | 3 | B. | $\frac{7}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
15.若$sinθcosθ=\frac{1}{2}$,则$tanθ-\frac{cosθ}{sinθ}$的值是( )
| A. | -2 | B. | 0 | C. | ±2 | D. | $\frac{1}{2}$ |
2.双曲线$\frac{x^2}{4}-\frac{y^2}{3}=1$的渐近线所在直线方程为( )
| A. | $x=±\frac{{\sqrt{3}}}{3}y$ | B. | $y=±\frac{{\sqrt{3}}}{3}x$ | C. | $y=±\frac{{\sqrt{3}}}{2}x$ | D. | $x=±\frac{{\sqrt{3}}}{2}y$ |