题目内容

矩阵
0-1
10
的逆矩阵是（　　）
A、
01
-10
B、
-10
01
C、
10
0-1
D、
0-1
10
考点：逆矩阵的意义
专题：矩阵和变换
分析：本题可以直接根据逆矩阵的定义求出逆矩阵．
解答： 解：设矩阵
0-1
10
的逆矩阵为
ab
cd
，
则
0-1
10
ab
cd
=
10
01
，
∴
-c=1
-d=0
a=0
b=1
，
∴
a=0
b=1
c=-1
d=0
，
∴矩阵
0-1
10
的逆矩阵为
01
-10
．
故选A．
点评：本题考查的是逆矩阵的定义，还可用逆矩阵的公式求解，本题属于基础题．
练习册系列答案
相关题目
高三毕业时，甲、乙、丙、丁四位同学站成一排照相留念，已知甲乙相邻，则甲丙相邻的概率为（　　）
A、
1
3
B、
2
3
C、
1
2
D、
1
6
已知平面向量
a
=（1，1），
b
=（1，-1），则向量
1
2
a
-
3
2
b
=（　　）
A、（-2，-1）
B、（-2，1）
C、（-1，0）
D、（-1，2）
对任意的x∈[-
1
2
，1]，不等式x2+2x-a≤0恒成立，则实数a的取值范围是（　　）
A、（-∞，0]
B、（-∞，3]
C、[0，+∞）
D、[3，+∞）
阅读下列算法程序框图，若输出的结果S为
3
，则判断框中的横线上最小正整数值为（　　）
A、1B、2C、3D、4
有下列四个表达式：
①|
a
+
b
|=|
a
|+|
b
|； ②|
a
-
b
|≥±（|
a
|-|
b
|）；③
a
2＞|
a
|2； ④|
a
•
b
|=|
a
|•|
b
|．
其中正确的个数为（　　）
A、0B、2C、3D、4
要得到函数y=2cos（2x-
π
3
）的图象，只需将函数y=2sin2x的图象（　　）
A、向右平移
π
6
个单位
B、向右平移
π
12
个单位
C、向左平移
π
12
个单位
D、向左平移
π
6
个单位
已知函数f（x）满足条件f（x+y）=f（x）+f（y）+xy，x，y∈N*，又f（1）=1，求f（x）．
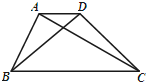如图，在梯形ABCD中，AD∥BC，AB=5，AC=9，∠BCA=30°，∠ADB=45°．
（Ⅰ）求sin∠ABC；
（Ⅱ）求BD的长度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网