题目内容
对于函数f(x)在定义域内的任意实数x及x+m(m>0),都有f(-x)+f(x)=0及f(x+m)>f(x)成立,则称函数f(x)为“Z函数”.现给出下列四个函数:g(x)=
u(x)=
h(x)=x+
;v(x)=cosx.其中是“Z函数”的是( )
|
|
| 1 |
| x |
| A、g(x) | B、h(x) |
| C、u(x) | D、v(x) |
考点:分段函数的应用
专题:新定义,数形结合,函数的性质及应用
分析:首先判断是否满足f(-x)+f(x)=0,只有y=g(x),y=h(x)满足,再将它们的图象向左平移,观察是否都在原图形的上方,如果是即为“Z函数”.
解答:
解:如图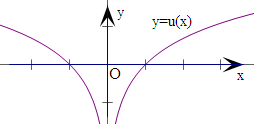 y=u(x)是偶函数,不满足f(-x)+f(x)=0;
y=u(x)是偶函数,不满足f(-x)+f(x)=0;
y=v(x)=cosx是偶函数,不满足f(-x)+f(x)=0;
y=g(x)如图满足f(-x)+f(x)=0,将y=g(x)的图象向左平移m个单位后,图象恒在原图象上方,即f(x+m)>f(x);
y=h(x)满足f(-x)+f(x)=0,将y=h(x)的图象向左平移m个单位后,图象不恒在原图象上方,即不满足f(x+m)>f(x);
故是“Z函数”的是y=g(x).
故选A.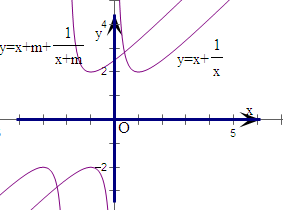
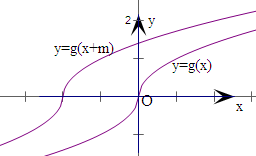
 y=u(x)是偶函数,不满足f(-x)+f(x)=0;
y=u(x)是偶函数,不满足f(-x)+f(x)=0;y=v(x)=cosx是偶函数,不满足f(-x)+f(x)=0;
y=g(x)如图满足f(-x)+f(x)=0,将y=g(x)的图象向左平移m个单位后,图象恒在原图象上方,即f(x+m)>f(x);
y=h(x)满足f(-x)+f(x)=0,将y=h(x)的图象向左平移m个单位后,图象不恒在原图象上方,即不满足f(x+m)>f(x);
故是“Z函数”的是y=g(x).
故选A.
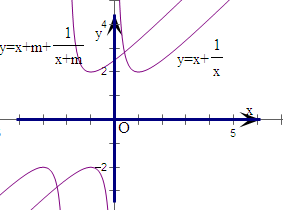
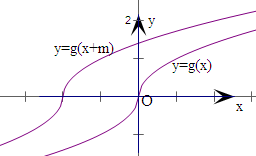
点评:本题考查分段函数的图象及应用,考查函数的性质和图象平移,考查数形结合的能力,属于中档题.

练习册系列答案
相关题目
已知A={x|2x-1≤3},则下列各式正确的是( )
| A、3∈A | B、2∈A |
| C、1∉A | D、0∉A |
函数f(x)的定义域为R,f(0)=0,且?x∈R,f′(x)≥2,则不等式f(x)≥2x的解集为( )
| A、[0,1] |
| B、[0,+∞) |
| C、(-∞,0] |
| D、[-1,1] |
某物体做直线运动,其运动规律是s=t2+
(t的单位是秒,s的单位是米),则它在4秒末的瞬时速度为( )
| 3 |
| t |
A、
| ||
B、
| ||
| C、8米/秒 | ||
D、
|
下列命题中正确的是( )
| A、若平面M外的两条直线在平面M内的射影为一条直线及此直线外的一个点,则这两条直线互为异面直线 |
| B、若平面M外的两条直线在平面M内的射影为两条平行直线,则这两条直线相交 |
| C、若平面M外的两条直线在平面M内的射影为两条平行直线,则这两条直线平行 |
| D、若平面M外的两条直线在平面M内的射影为两条互相垂直的直线,则这两条直线垂直 |