题目内容
1.在正方体ABCD-A1B1C1D1中,下列几种说法正确的是( )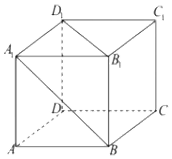
| A. | A1B∥D1B | B. | AC1⊥B1C | ||
| C. | A1B与平面DBD1B1成角为45° | D. | A1B,B1C成角为30° |
分析 由图可知A错误;由线面垂直的判定与性质可B正确;分别求出线面角及异面直线所成角判定C、D错误.
解答 解:如图,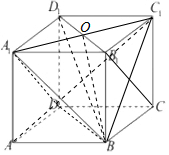
A1B∩D1B=B,故A错误;
连接BC1,则BC1⊥B1C,又AB⊥B1C,AB∩BC1=B,
∴B1C⊥平面ABC1,则AC1⊥B1C,故B正确;
连接A1C1,交B1D1=O,连接BO,则∠A1BO为A1B与平面DBD1B1成角,
在Rt△A1OB中,sin$∠{A}_{1}BO=\frac{1}{2}$,∴A1B与平面DBD1B1成角为30°,故C错误;
连接A1D,则A1D∥B1C,连接BD,可得△A1BD为等边三角形,则∠A1DB为60°,
即A1B,B1C成角为60°,故D错误.
故选:B.
点评 本题考查空间中直线与直线、直线与平面的位置关系,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
12.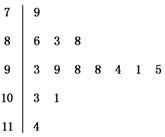 如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
 如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )| A. | 98 | B. | 94 | C. | 94.5 | D. | 95 |
6.已知椭圆C:$\frac{x^2}{25}+\frac{y^2}{b^2}=1({0<b<5})$的长轴长、短轴长、焦距成等差数列,则该椭圆的方程是( )
| A. | $\frac{x^2}{25}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{25}+{y^2}=1$ |
13.函数f(x)=x+cosx在[0,π]上的最小值为( )
| A. | -2 | B. | 0 | C. | -$\frac{1}{2}$ | D. | 1 |
11.若正三棱柱的所有棱长均为4,则其体积为( )
| A. | $\frac{{16\sqrt{3}}}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $8\sqrt{3}$ | D. | $16\sqrt{3}$ |
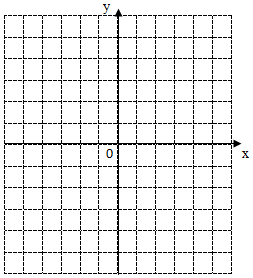 试写出函数f(x)=x${\;}^{\frac{1}{2}}$的性质,并作出它的大致图象.
试写出函数f(x)=x${\;}^{\frac{1}{2}}$的性质,并作出它的大致图象.