题目内容
10.已知圆C的方程为:x2+y2=9,过圆C上一动点M作平行于y轴的直线m,设m与x轴的交点为N,若向量$\overrightarrow{OQ}=\overrightarrow{OM}+\overrightarrow{ON}$,则动点Q的轨迹方程是$\frac{x^2}{4}+{y^2}=9$.分析 设Q(x,y),M(s,t),则N(0,t),由于向量$\overrightarrow{OQ}=\overrightarrow{OM}+\overrightarrow{ON}$,利用向量相等可得$\left\{\begin{array}{l}{x=s}\\{y=2t}\end{array}\right.$,解出s,t再代入圆的方程即可.
解答 解:设Q(x,y),M(s,t),则N(0,t),s2+t2=9.(*)
∵向量$\overrightarrow{OQ}=\overrightarrow{OM}+\overrightarrow{ON}$,(O为原点),∴$\left\{\begin{array}{l}{x=s}\\{y=2t}\end{array}\right.$,
解得$\left\{\begin{array}{l}{s=x}\\{t=y}\end{array}\right.$,代入(*)化为$\frac{x^2}{4}+{y^2}=9$.
故答案为$\frac{x^2}{4}+{y^2}=9$.
点评 本题考查了轨迹方程,考查代点法,属于中档题.

练习册系列答案
相关题目
20.若m<n,p<q,且(p-m)(p-n)<0,(q-m)(q-n)<0,则m,n,p,q从小到大排列顺序是( )
| A. | m<p<q<n | B. | p<m<q<n | C. | m<p<n<q | D. | p<m<n<q |
1.在正方体ABCD-A1B1C1D1中,下列几种说法正确的是( )
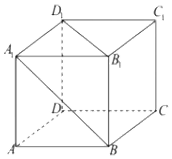

| A. | A1B∥D1B | B. | AC1⊥B1C | ||
| C. | A1B与平面DBD1B1成角为45° | D. | A1B,B1C成角为30° |
5.过抛物线y2=4ax(a>0)的焦点F作斜率为-1的直线l,l与离心率为e的双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({b>0})$的两条渐近线的交点分别为B,C.若xB,xC,xF分别表示B,C,F的横坐标,且$x_F^2=-{x_B}•{x_C}$,则e=( )
| A. | 6 | B. | $\sqrt{6}$ | C. | 3 | D. | $\sqrt{3}$ |
2.已知全集U={1,2,3,4,5,6,7},集合A={1,3,5,6,7},B={1,2,3,4,6,7},则A∩∁UB=( )
| A. | {3,6} | B. | {5} | C. | {2,4} | D. | {2,5} |
19.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{6}}}{2}$,则它的渐近线方程为( )
| A. | y=±2x | B. | y=±$\frac{1}{4}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{{\sqrt{2}}}{2}$x |