题目内容
已知在△ABC中,∠ABC=40°,∠ACB=30°,P为∠ABC的平分线上,∠PCA=20°,BP交AC于点M,CP交AB于点N.求证:PM=NA.
考点:解三角形的实际应用
专题:解三角形
分析:在BA延长线上取一点D,使BD=BC,连接DP,DC.由于BP平分∠ABC,由对称性可得PD=PC.∠DPC=60°,△PDC是正三角形.在△ACD中,根据∠ADC=70°=∠CAD,可得AC=DC.在△PCA中,由∠PCA=20°,可知∠PAC=80°.从而∠PAB=30°.在△AMP中,由正弦定理可得:
=
.在△ANP中,由正弦定理可得:
=
.即可得出.
| PM |
| sin80° |
| PA |
| sin50° |
| AN |
| sin100° |
| PA |
| sin50° |
解答:
证明:在BA延长线上取一点D,使BD=BC,连接DP,DC.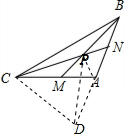
∵BP平分∠ABC,
可知C点与点D关于BP对称,
∴PD=PC.
∵∠DPC=2(∠PBC+∠PCB)=60°,
∴△PDC是正三角形,PC=DC.
在△ACD中,∵∠ADC=70°=∠CAD,
∴AC=DC,
∴AC=PC.
在△PCA中,∵∠PCA=20°,
∴∠PAC=80°.
∴∠PAB=∠BAC-∠PCA=110°-80°=30°.
在△AMP中,由正弦定理可得:
=
.
在△ANP中,由正弦定理可得:
=
.
∴PM=AN.

∵BP平分∠ABC,
可知C点与点D关于BP对称,
∴PD=PC.
∵∠DPC=2(∠PBC+∠PCB)=60°,
∴△PDC是正三角形,PC=DC.
在△ACD中,∵∠ADC=70°=∠CAD,
∴AC=DC,
∴AC=PC.
在△PCA中,∵∠PCA=20°,
∴∠PAC=80°.
∴∠PAB=∠BAC-∠PCA=110°-80°=30°.
在△AMP中,由正弦定理可得:
| PM |
| sin80° |
| PA |
| sin50° |
在△ANP中,由正弦定理可得:
| AN |
| sin100° |
| PA |
| sin50° |
∴PM=AN.
点评:本题考查了角平分线的对称性、等边三角形的性质、正弦定理的应用、三角形的外角性质定理,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知集合A={1,2,3},B={2,3,4,5},则A∪B=( )
| A、{6,7,8} |
| B、{1,4,5,6,7,8} |
| C、{2,3} |
| D、{1,2,3,4,5} |
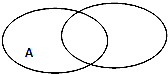
如图中阴影部分表示的集合是( )


| A、∁U(A∪B) |
| B、A∩(∁UB) |
| C、∁U(A∩B) |
| D、∁B(A∩B) |
 已知A=
已知A=