题目内容
设函数f(x)=
cos2ωx+sinωxcosωx(ω,a∈R),已知f(x)的图象在y轴右侧的第一个最高点的横坐标为
.
(1)求ω的值;
(2)若函数y=f(x)的图象按向量
=(
,
)平移后得到函数y=g(x)的图象,求y=g(x)在区间[0,
]的值域.
| 3 |
| π |
| 6 |
(1)求ω的值;
(2)若函数y=f(x)的图象按向量
| b |
| π |
| 6 |
| ||
| 2 |
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)化简f(x),由f(x)的图象在y轴右侧的第一个最高点的横坐标,求出ω的值;
(2)由f(x)按向量
平移后得g(x)的解析式,求出x∈[0,
]时g(x)的值域即可.
(2)由f(x)按向量
| b |
| π |
| 2 |
解答:
解:(1)∵f(x)=
cos2ωx+sinωxcosωx
=
cos2ωx+
sin2ωx+
=sin(2ωx+
)+
,
令2ω×
+
=
,
解得ω=
;
(2)∵f(x)=sin(x+
)+
,
按向量
=(
,
)平移后,
得g(x)=sin(x+
)+
,
又∵x∈[0,
],
∴x+
∈[
,
],
∴sin(x+
)∈[
,1];
∴g(x)的值域是[
+
,1+
].
| 3 |
=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=sin(2ωx+
| π |
| 3 |
| ||
| 2 |
令2ω×
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
解得ω=
| 1 |
| 2 |
(2)∵f(x)=sin(x+
| π |
| 3 |
| ||
| 2 |
按向量
| b |
| π |
| 6 |
| ||
| 2 |
得g(x)=sin(x+
| π |
| 6 |
| 3 |
又∵x∈[0,
| π |
| 2 |
∴x+
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
∴sin(x+
| π |
| 6 |
| 1 |
| 2 |
∴g(x)的值域是[
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查了三角函数的图象与性质的应用问题,也考查了图象平移的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
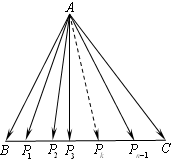 若在边长为1的正三角形△ABC的边BC上有n(n∈N*,n≥2)等分点,沿向量
若在边长为1的正三角形△ABC的边BC上有n(n∈N*,n≥2)等分点,沿向量| BC |
| AB |
| AP1 |
| AP1 |
| AP2 |
| APn-1 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列关于频率与概率的关系表示正确的是( )
| A、频率就是概率 |
| B、频率是客观存在的,与试验次数无关 |
| C、概率是随机的,在实验前不能确定 |
| D、随着试验次数的增加,频率一般会越来越接近概率 |
 已知y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,当x>0时,f(x)=log2x,
已知y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,当x>0时,f(x)=log2x,