题目内容

已知函数f（x）=ex（x2+ax-a+1），其中a是常数．
（1）当a=1时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）若f（x）在定义域内是单调递增函数，求a的取值范围．
考点：利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题：导数的综合应用
分析：（1）求出导数，求出切点和切线的斜率，由点斜式方程，即可得到切线方程；
（2）由（1）求得的导数，若f（x）是单调递增函数，则f′（x）≥0恒成立，运用判别式不大于0，即可得到；
解答： 解：（1）由f（x）=ex（x2+ax-a+1）可得f′（x）=ex[x2+（a+2）x+1]．
当a=1时，f（1）=2e，f′（1）=5e
故曲线y=f（x）在点（1，f（1））处的切线方程为y-2e=5e（x-1），
即5ex-y-3e=0；
（2）由（1）知f′（x）=ex[x2+（a+2）x+1]，
若f（x）是单调递增函数，则f′（x）≥0恒成立，
即x2+（a+2）x+1≥0恒成立，
∴△=（a+2）2-4≤0，-4≤a≤0，
故a的取值范围为[-4，0]．
点评：本题主要考查导数的几何意义以及函数单调性和导数之间的关系，综合考查导数的应用．
练习册系列答案
相关题目
2sin5°-cos25°
sin25°
的值是
 
．
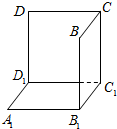如图是从上下底面处在水平状态下的棱长为1m的正方体ABCD-A1B1C1D1中分离出来的．如果用图示中这样一个装置来盛水，那么最多能盛
 
m3体积的水．
已知数列{an}，其满足条件a1=
5
3
，3an+1-2an=2n+5，
（1）求证：数列{an-2n+1}为等比数列；
（2）已知Sn为数列{an}的前n项和，对一切n∈N*，有不等式Sn≥log2m+1恒成立，求实数m的取值范围．
设函数f（x）=
3
cos2ωx+sinωxcosωx（ω，a∈R），已知f（x）的图象在y轴右侧的第一个最高点的横坐标为
π
6
．
（1）求ω的值；
（2）若函数y=f（x）的图象按向量
b
=（
π
6
，
3
2
）平移后得到函数y=g（x）的图象，求y=g（x）在区间[0，
π
2
]的值域．
直线y=ax-3a+2（a∈R）必过定点
 
．
已知定义在区间[
b
a
，
d
c
]上的函数f（x）=
ax-b
+
d-cx
（a＞0，c＞0）具有如下性质：f（x）在区间[
b
a
，x0]上单调递增，f（x）在区间[x0，
d
c
]上单调递减，且f（x）max=f（x0）（其中x0=
b
a
+
d
c
-
b+d
a+c
）．现给定函数f（x）=
8x-16
+
36-9x
，请你根据上述知识解决下列问题：
（1）求出f（x）的定义域；
（2）对于任意的x1，x2∈[2，
50
17
]，当x1＜x2时，比较f（x1）和f（x2）的大小；
（3）若f（x）-m＜0的解集为非空集合，求整数m的最小值．
如图所示，一个空间几何体的正视图和侧视图都是边长为2的正方形，俯视图是一个圆，那么这个几何体的表面积为（　　）
A、3πB、4πC、5πD、6π
曲线C的极坐标方程为ρsin2θ=cosθ，曲线F 的参数方程为
x=3-t
y+t=1
，以极点为原点，极轴为x正半轴建立直角坐标系，则曲线C与曲线F有
 
个公共点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网