题目内容
长为6米、宽为4米的矩形,当长增加x米,且宽减少
米时面积最大,此时宽减少了 米,面积取得了最大值.
| x |
| 2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:根据已知条件设矩形的面积为y,则y=(6+x)(4-
)=-
x2+x+24,对该二次函数进行配方即可得到y取最大值时x的取值,从而求出
,即求出宽度减少的米数.
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
解答:
解:由题意有,设面积为y,则:
y=(6+x)(4-
)=-
x2+x+24=-
(x-1)2+
,(0<x<8);
∴x=1时,y取到最大值,此时宽度减少了
米.
故答案为:
.
y=(6+x)(4-
| x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 49 |
| 2 |
∴x=1时,y取到最大值,此时宽度减少了
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查数学建模能力,以及二次函数求最直点的方法.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
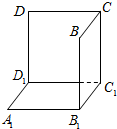 如图是从上下底面处在水平状态下的棱长为1m的正方体ABCD-A1B1C1D1中分离出来的.如果用图示中这样一个装置来盛水,那么最多能盛
如图是从上下底面处在水平状态下的棱长为1m的正方体ABCD-A1B1C1D1中分离出来的.如果用图示中这样一个装置来盛水,那么最多能盛