题目内容
下列四个命题中的假命题是( )
| A、?x∈R,ex≥x+1 | ||
| B、?x∈R,e-x≥-x+1 | ||
| C、?x0>0,lnx0>x0-1 | ||
D、?x0>0,ln
|
考点:命题的真假判断与应用
专题:导数的概念及应用,导数的综合应用,简易逻辑
分析:分别构造对应的函数,并利用导数法分析函数的最值,进而可逐一判断出四个答案中对应命题的真假,得到结论.
解答:
解:对于A,令f(x)=ex-x-1,则f′(x)=ex-1,
当x>0时,f′(x)>0,f(x)为增函数,
当x<0时,f′(x)<0,f(x)为减函数,
故当x=0时,f(x)取最小值0,即f(x)≥0恒成立,
即?x∈R,ex≥x+1,故正确;
对于B,令f(x)=e-x+x-1,则f′(x)=-e-x+1,
当x>0时,f′(x)>0,f(x)为增函数,
当x<0时,f′(x)<0,f(x)为减函数,
故当x=0时,f(x)取最小值0,即f(x)≥0恒成立,
即?x∈R,e-x≥-x+1,故正确;
对于B,令f(x)=lnx-x+1,则f′(x)=
-1,
当x>1时,f′(x)<0,f(x)为减函数,
当x<1时,f′(x)>0,f(x)为增函数,
故当x=1时,f(x)取最大值0,即f(x)≤0恒成立,
即?x∈R,lnx≤x-1,故错误;
对于D,由C答案的分析过程得:当x>0且x≠1时,lnx<x-1,
即?x0>0,使lnx0<x0-1,即-lnx0<-x0+1,即ln
>-x0+1,故正确;
故选:C
当x>0时,f′(x)>0,f(x)为增函数,
当x<0时,f′(x)<0,f(x)为减函数,
故当x=0时,f(x)取最小值0,即f(x)≥0恒成立,
即?x∈R,ex≥x+1,故正确;
对于B,令f(x)=e-x+x-1,则f′(x)=-e-x+1,
当x>0时,f′(x)>0,f(x)为增函数,
当x<0时,f′(x)<0,f(x)为减函数,
故当x=0时,f(x)取最小值0,即f(x)≥0恒成立,
即?x∈R,e-x≥-x+1,故正确;
对于B,令f(x)=lnx-x+1,则f′(x)=
| 1 |
| x |
当x>1时,f′(x)<0,f(x)为减函数,
当x<1时,f′(x)>0,f(x)为增函数,
故当x=1时,f(x)取最大值0,即f(x)≤0恒成立,
即?x∈R,lnx≤x-1,故错误;
对于D,由C答案的分析过程得:当x>0且x≠1时,lnx<x-1,
即?x0>0,使lnx0<x0-1,即-lnx0<-x0+1,即ln
| 1 |
| x0 |
故选:C
点评:本题以命题的真假判断为载体,考查了导数法研究函数单调性和最值的方法,综合性强,难度较大,属于难题.

练习册系列答案
相关题目
函数f(x)=Asin(ωx+φ)(A≠0,ω≠0),则f(x) ( )
| A、是非奇函数非偶函数 |
| B、奇偶性与φ有关 |
| C、奇偶性与ω有关 |
| D、奇偶性与A有关 |
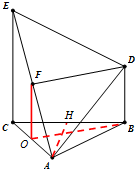 如图,在多面体ECABD中,EC⊥平面ABC,DB∥EC,△ABC为正三角形,F为EA的中点,EC=AC=2,BD=1.
如图,在多面体ECABD中,EC⊥平面ABC,DB∥EC,△ABC为正三角形,F为EA的中点,EC=AC=2,BD=1. 已知三角形△ABC的三个顶点分别为A(-1,0),B(1,0),C(0,1).
已知三角形△ABC的三个顶点分别为A(-1,0),B(1,0),C(0,1).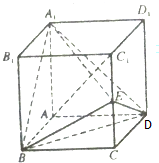 如图,在正方体ABCD-A1B1C1D1中,点E在棱CC1上.
如图,在正方体ABCD-A1B1C1D1中,点E在棱CC1上.