题目内容
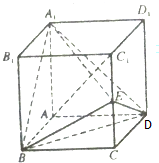 如图,在正方体ABCD-A1B1C1D1中,点E在棱CC1上.
如图,在正方体ABCD-A1B1C1D1中,点E在棱CC1上.(1)求证:A1E⊥BD;
(2)若E为棱CC1的中点,求证:AC1∥平面BED;
(3)当
| CE |
| CC1 |
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连结AC,BD,由已知得AC⊥BD,AA1⊥BD,从而BD⊥平面ACC1A1,由此能证明A1E⊥BD.
(2)连结AC,BD,交于点O,连结OE,则OE∥AC1,由此能证明AC1∥平面BED.
(3)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,由此利用向量法能求出
=
时,二面角A1-BD-E为直二面角.
(2)连结AC,BD,交于点O,连结OE,则OE∥AC1,由此能证明AC1∥平面BED.
(3)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,由此利用向量法能求出
| CE |
| CC1 |
| 1 |
| 2 |
解答:
(1)证明:连结AC,BD,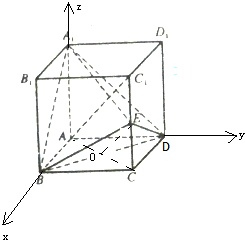
∵ABCD是正方形,∴AC⊥BD,
∵在正方体ABCD-A1B1C1D1中,AA1⊥BD,
又AA1∩AC=A,∴BD⊥平面ACC1A1,
∵A1E?平面ACC1A1,∴A1E⊥BD.
(2)证明:连结AC,BD,交于点O,连结OE,
∵ABCD是正方形,∴O是AC的中点,
∵E是CC1中点,∴OE∥AC1,
∵OE?平面BED,AC1?平面BED,
∴AC1∥平面BED.
(3)解:以A为原点,AB为x轴,AD为y轴,AA1为z轴,
建立空间直角坐标系,
设正方体ABCD-A1B1C1D1的棱长为1,CF=t(0≤t≤1),
A1(0,0,1),B(1,0,0),D(0,1,0),E(1,1,t),
=(1,0,-1),
=(0,1,-1),
设平面A1BD的法向量
=(x,y,z),
则
,取x=1,得
=(1,1,1),
=(-1,1,0),
=(0,1,t),
设平面BED的法向量
=(a,b,c),
则
,取a=1,得
=(1,1,-
),
∵二面角A1-BD-E为直二面角,
∴
•
=1+1-
=0,解得t=
,
∴CF=
,∴
=
时,二面角A1-BD-E为直二面角.

∵ABCD是正方形,∴AC⊥BD,
∵在正方体ABCD-A1B1C1D1中,AA1⊥BD,
又AA1∩AC=A,∴BD⊥平面ACC1A1,
∵A1E?平面ACC1A1,∴A1E⊥BD.
(2)证明:连结AC,BD,交于点O,连结OE,
∵ABCD是正方形,∴O是AC的中点,
∵E是CC1中点,∴OE∥AC1,
∵OE?平面BED,AC1?平面BED,
∴AC1∥平面BED.
(3)解:以A为原点,AB为x轴,AD为y轴,AA1为z轴,
建立空间直角坐标系,
设正方体ABCD-A1B1C1D1的棱长为1,CF=t(0≤t≤1),
A1(0,0,1),B(1,0,0),D(0,1,0),E(1,1,t),
| A1B |
| A1D |
设平面A1BD的法向量
| n |
则
|
| n |
| BD |
| BE |
设平面BED的法向量
| m |
则
|
| m |
| 1 |
| t |
∵二面角A1-BD-E为直二面角,
∴
| m |
| n |
| 1 |
| t |
| 1 |
| 2 |
∴CF=
| 1 |
| 2 |
| CE |
| CC1 |
| 1 |
| 2 |
点评:本题考查异面直线垂直的证明,考查直线与平面平行的证明,考查使二面角为直二面角的线段的比值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
下列四个命题中的假命题是( )
| A、?x∈R,ex≥x+1 | ||
| B、?x∈R,e-x≥-x+1 | ||
| C、?x0>0,lnx0>x0-1 | ||
D、?x0>0,ln
|
已知一个三棱柱的三视图如图所示,则该三棱柱的体积为( )


A、
| ||
B、
| ||
C、
| ||
| D、1 |
 如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是∠ADC=60°的菱形,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是∠ADC=60°的菱形,M为PB的中点.