题目内容
在平面直角坐标系中,已知点O(0,0),A(3,0),B(0,3),C(cosα,sinα),D(-2cosα,-1),其中α∈(
,
)
(1)若
•
=-1,求
的值;
(2)若f(α)=
•
-t2+2在定义域α∈(
,
)有最小值-1,求t的值.
| π |
| 2 |
| 3π |
| 2 |
(1)若
| AC |
| BC |
| 2sin2α+2sinαcosα |
| 1+tanα |
(2)若f(α)=
| OC |
| OD |
| π |
| 2 |
| 3π |
| 2 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的图像与性质
分析:(1)结合平面向量的坐标表示,写出
,
的坐标表示,然后,根据向量的数量积的运算,得到cosα+sinα=
,然后,结合二倍角公式进行求解;
(2)采用二次函数思想进行求解.
| AC |
| BC |
| 2 |
| 3 |
(2)采用二次函数思想进行求解.
解答:
解:(1)根据已知,
=(cosα-3,sinα)
=(cosα,sinα-3)
∴
•
=cos2α-3cosα+sin2α-3sinα=-1
∴1-3(cosα+sinα)=-1
∴cosα+sinα=
平方得到cos2α+2cosαsinα+sin2α=1+2cosαsinα=
∴2cosαsinα=-
,
∴
=2cosαsinα=-
,
(2)f(α)=-2cos2α-tsinα-t2+2=2sin2α-tsinα-t2
=2(sinα-
)2-
,
设sinα=m,
∵α∈(
,
),
∴m∈(-1,1),
∴f(m)=2(m-
)2-
,
①当
≤-1时,即t≤-4,此时,函数无最小值;
②当
≥1时,即t≥4,此时,函数无最小值;
③当-1<
<1时,即-4<t<4,此时,函数当sinα=
时取得,为-
,
∴-
=-1,
∴t=±
,
同时
=±
∈(-1,1),
∴t=±
满足题意.
| AC |
| BC |
∴
| AC |
| BC |
∴1-3(cosα+sinα)=-1
∴cosα+sinα=
| 2 |
| 3 |
平方得到cos2α+2cosαsinα+sin2α=1+2cosαsinα=
| 4 |
| 9 |
∴2cosαsinα=-
| 5 |
| 9 |
∴
| 2sin2α+2sinαcosα |
| 1+tanα |
| 5 |
| 9 |
(2)f(α)=-2cos2α-tsinα-t2+2=2sin2α-tsinα-t2
=2(sinα-
| t |
| 4 |
| 9t2 |
| 8 |
设sinα=m,
∵α∈(
| π |
| 2 |
| 3π |
| 2 |
∴m∈(-1,1),
∴f(m)=2(m-
| t |
| 4 |
| 9t2 |
| 8 |
①当
| t |
| 4 |
②当
| t |
| 4 |
③当-1<
| t |
| 4 |
| t |
| 4 |
| 9t2 |
| 8 |
∴-
| 9t2 |
| 8 |
∴t=±
2
| ||
| 3 |
同时
| t |
| 4 |
| ||
| 6 |
∴t=±
2
| ||
| 3 |
点评:本题综合考查了平面向量的坐标运算,二倍角公式,三角恒等变换等公式,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
函数f(x)=x-sinx是( )
| A、奇函数且单调递增 |
| B、奇函数且单调递减 |
| C、偶函数且单调递增 |
| D、偶函数且单调递减 |
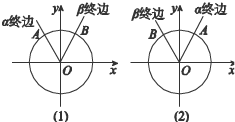 如图,在平面直角坐标系xOy内作单位圆O,以Ox为始边作任意角α,β,它们的终边与单位圆O的交点分别为A,B,
如图,在平面直角坐标系xOy内作单位圆O,以Ox为始边作任意角α,β,它们的终边与单位圆O的交点分别为A,B,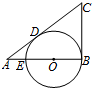 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则BC的长为
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则BC的长为