题目内容
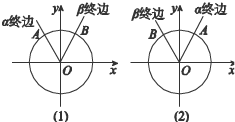 如图,在平面直角坐标系xOy内作单位圆O,以Ox为始边作任意角α,β,它们的终边与单位圆O的交点分别为A,B,
如图,在平面直角坐标系xOy内作单位圆O,以Ox为始边作任意角α,β,它们的终边与单位圆O的交点分别为A,B,(1)设α=105°,β=75°,求
| OA |
| OB |
(2)试证明两角差的余弦公式C(α-β);cos(α-β)=cosαcosβ+sinαsinβ.
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:(1)由题意推出点A(cosα,sinα),B(cosβ,sinβ),利用两角差的余弦函数直接求解即可.
(2)在平面直角坐标系中,以原点为圆心,作一单位圆,再以原点为顶点,x轴非负半轴为始边分别作角α,β.设它们的终边分别交单位圆于点P1(cosα,sinα),P2(cosβ,sinβ),即有两单位向量
,
,它们的所成角是|α-β|,根据向量数量积的性质能够证明cos(α-β)=cosαcosβ+sinαsinβ.
(2)在平面直角坐标系中,以原点为圆心,作一单位圆,再以原点为顶点,x轴非负半轴为始边分别作角α,β.设它们的终边分别交单位圆于点P1(cosα,sinα),P2(cosβ,sinβ),即有两单位向量
| OA |
| OB |
解答:
解:(1)在平面直角坐标系中,以原点为圆心, 作一单位圆,
作一单位圆,
再以原点为顶点,x轴非负半轴为始边分别作角α=105°,β=75°.
设它们的终边分别交单位圆于点A(cosα,sinα),B(cosβ,sinβ),
•
=cos105°cos75°+sin105°sin75°
=cos(105°-75°)=cos30°=
.
(2)如图,在平面直角坐标系中,以原点为圆心, 作一单位圆,再以原点为顶点,x轴非负半轴为始边分别作角α,β.
作一单位圆,再以原点为顶点,x轴非负半轴为始边分别作角α,β.
设它们的终边分别交单位圆于点A(cosα,sinα),B(cosβ,sinβ),…(4分)
即有两单位向量
,
,
它们的所成角是|α-β|,
根据向量数量积的性质得:
•
=cos(α-β)=cos|α-β|①
又根据向量数量积的坐标运算得:
•
=cosαcosβ+sinαsinβ②
由①②得 cos(α-β)=cosαcosβ+sinαsinβ.
 作一单位圆,
作一单位圆,再以原点为顶点,x轴非负半轴为始边分别作角α=105°,β=75°.
设它们的终边分别交单位圆于点A(cosα,sinα),B(cosβ,sinβ),
| OA |
| OB |
=cos(105°-75°)=cos30°=
| ||
| 2 |
(2)如图,在平面直角坐标系中,以原点为圆心,
 作一单位圆,再以原点为顶点,x轴非负半轴为始边分别作角α,β.
作一单位圆,再以原点为顶点,x轴非负半轴为始边分别作角α,β.设它们的终边分别交单位圆于点A(cosα,sinα),B(cosβ,sinβ),…(4分)
即有两单位向量
| OA |
| OB |
它们的所成角是|α-β|,
根据向量数量积的性质得:
| OA |
| OB |
又根据向量数量积的坐标运算得:
| OA |
| OB |
由①②得 cos(α-β)=cosαcosβ+sinαsinβ.
点评:本题考查平面向量的综合应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,利用三角函数的性质合理地进行等价转化.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
a,b∈R,则“a=2b”是“复数
为纯虚数”的( )
| a+bi |
| 1-2i |
| A、充分而不必要条件 |
| B、必要不充分条件 |
| C、抽样条件 |
| D、既不充分也不必要条件 |