题目内容
4.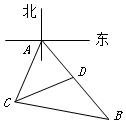 为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.
为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.
分析 由图形求出∠CAD的度数,以及BC,BD及CD的长,利用余弦定理求出cosB的值,再利用同角三角函数间的基本关系求出sinB的值,由sinA,sinB及BC的长,利用正弦定理求出AC的长,由BC,AC及cosA的值,利用余弦定理求出AB的长,由AB-BD即可求出AD的长.
解答 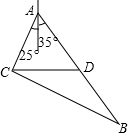 解:如图,易知∠CAD=25°+35°=60°,BC=31,BD=20,CD=21,
解:如图,易知∠CAD=25°+35°=60°,BC=31,BD=20,CD=21,
由余弦定理得:cosB=$\frac{B{C}^{2}+B{D}^{2}}{2SC•BD}$=$\frac{3{1}^{2}+2{0}^{2}-2{1}^{2}}{2×31×20}$=$\frac{23}{31}$,
∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{12\sqrt{3}}{31}$,
又在△ABC中,由正弦定理得:AC=$\frac{BCsinB}{sinA}$=$\frac{32×\frac{12\sqrt{3}}{31}}{\frac{\sqrt{3}}{2}}$=24,
由余弦定理得BC2=AC2+AB2-2AC•ABcosA,即312=AB2+242-2×AB×24cos60°,
∴AB2-24AB-385=0,
解得:AB=35或AB=-11(舍去),
∴AD=AB-BD=35-20=15(km).
点评 此题考查了余弦定理,正弦定理,以及同角三角函数间的基本关系,熟练掌握正弦、余弦定理的解本题的关键.

练习册系列答案
相关题目
12.已知定义在R上的函数f(x)为周期函数,且周期为4,若在区间[-2,2]上,f(x)=$\left\{\begin{array}{l}{{2}^{x}+2m,-2≤x≤0}\\{lo{g}_{2}x-m,0<x≤2}\end{array}\right.$,则f(2017m)=( )
| A. | -$\frac{9}{4}$ | B. | -$\frac{5}{2}$ | C. | $\frac{9}{4}$ | D. | $\frac{5}{2}$ |
9.以下函数中在区间(0,+∞)上单调递增的函数是( )
| A. | y=|x|+1 | B. | y=$\frac{1}{x}$ | C. | y=-x2+1 | D. | y=-x|x| |
13.抛物线x=4y2的焦点坐标是( )
| A. | (0,1) | B. | (0,-1) | C. | $({-\frac{1}{16},0})$ | D. | $({\frac{1}{16},0})$ |
14.设f(x)=x•lnx,若$f'({x_0})=\frac{3}{2}$,则x0=( )
| A. | $\sqrt{e}$ | B. | $-\sqrt{e}$ | C. | e2 | D. | $\frac{1}{e^2}$ |
 如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.