题目内容
9．以下函数中在区间（0，+∞）上单调递增的函数是（ ）| A． | y=|x|+1 | B． | y=$\frac{1}{x}$ | C． | y=-x2+1 | D． | y=-x|x| |
分析 分别判断函数在区间（0，+∞）上单调性，即可得出结论．
解答 解：对于A，在区间（0，+∞）上单调递增，正确；
对于B，在区间（0，+∞）上单调递减，不正确；
对于C，在区间（0，+∞）上单调递减，不正确；
对于D，x＞0，y=-x2，在区间（0，+∞）上单调递减，不正确；
故选：A．
点评 本题考查函数的单调性，考查学生对概念的理解，比较基础．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
16．
矩形ABCD中，$AB=\sqrt{3}$，BC=1，将△ABC与△ADC沿AC所在的直线进行随意翻折，在翻折过程中直线AD与直线BC成的角范围（包含初始状态）为（ ）
矩形ABCD中，$AB=\sqrt{3}$，BC=1，将△ABC与△ADC沿AC所在的直线进行随意翻折，在翻折过程中直线AD与直线BC成的角范围（包含初始状态）为（ ）| A． | $[0，\frac{π}{6}]$ | B． | $[0，\frac{π}{3}]$ | C． | $[0，\frac{π}{2}]$ | D． | $[0，\frac{2π}{3}]$ |
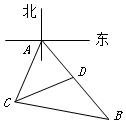为了考核某特警部队的应急反应能力，拟准备把特警队员从一目标处快速运送到另一目标处．通过测角仪观测到观测站C在目标A南偏西25°的方向上，B、D在A出发的一条南偏东35°走向的公路上（如图），测得C、B相距31千米，D、B相距20千米，C、D相距21千米，求A、D之间的距离．
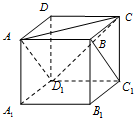在正方体ABCD-A1B1C1D1中（如图），已知点P在直线BC1上运动，则下列四个命题：
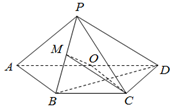如图，在四棱锥P-ABCD中，底面ABCD为梯形，AD∥BC，AB=BC=CD=1，DA=2，DP⊥平面ABP，O，M分别是AD，PB的中点．
18．已知集合A={x|ax2+x-3=0}，B={x|3≤x＜7}，若A∩B≠∅，则实数a的取值集合为（ ）
| A． | $[-\frac{1}{12}，-\frac{4}{49}）$ | B． | $[-\frac{1}{12}，0]$ | C． | $（-\frac{4}{49}，0]$ | D． | $[-\frac{4}{49}，0]$ |