题目内容

12．已知定义在R上的函数f（x）为周期函数，且周期为4，若在区间[-2，2]上，f（x）=$\left\{\begin{array}{l}{{2}^{x}+2m，-2≤x≤0}\\{lo{g}_{2}x-m，0＜x≤2}\end{array}\right.$，则f（2017m）=（　　）
A．-$\frac{9}{4}$B．-$\frac{5}{2}$C．$\frac{9}{4}$D．$\frac{5}{2}$

分析 利用定义在R上的函数f（x）为周期函数，且周期为4，求出m，再计算f（2017m）．

解答 解：因为定义在R上的函数f（x）为周期函数，且周期为4，所以f（-2）=f（2），故$\frac{1}{4}$+2m=1-m，解得m=$\frac{1}{4}$．
所以f（2017m）=f（$\frac{2017}{4}$）=f（$\frac{1}{4}$）=-2-$\frac{1}{4}$=-$\frac{9}{4}$．
故选A．

点评 本题考查函数的周期性，考查学生的计算能力，正确求出m是关键．

练习册系列答案
相关题目
19．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的离心率为2，坐标原点到直线AB的距离为$\frac{\sqrt{3}}{2}$，其中A（0，-b），B（a，0）．
（1）求双曲线的标准方程；
（2）设F是双曲线的右焦点，直线l过点F且与双曲线的右支交于不同的两点P、Q，|PQ|=10．求直线l的方程．
3．某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，220），[220，240），[240，260），[260，280），[280，300）分组的频率分布直方图如图．

（1）求直方图中x的值．
（2）求月平均用电量不大于220度的居民有多少户．
（3）在月平均用电量为[220，240），[240，260），[260，280），[280，300）的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220，240）的用户中应抽取多少户？
20．函数$f（x）=\frac{{\sqrt{2x-1}}}{{{x^2}+x-2}}$的定义域是$\left\{{x\left|{x≥\frac{1}{2}，且x≠1}\right.}\right\}$．
7．已知函数f（x）=$\sqrt{3}$sin2x-2cos2x+1．
（1）求函数f（x）在区间[-$\frac{π}{12}$，$\frac{π}{2}$）上的值域；
（2）设$α，β∈（{0，\frac{π}{2}}），f（{\frac{1}{2}α+\frac{π}{12}}）=\frac{10}{13}，f（{\frac{1}{2}β+\frac{π}{3}}）=\frac{6}{5}$，求sin（α-β）的值．
17．已知函数f（x）=x2+（a+1）x+（a+2）
（1）若f（x）能表示成一个奇函数g（x）和一个偶函数h（x）的和，求g（x）和h（x）的解析式．
（2）命题p：函数f（x）在区间[（a+1）2，+∞）上是增函数；命题q：函数g（x）是减函数．如果命题￢p，p∨q都是假命题，求a的取值范围．
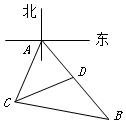4．为了考核某特警部队的应急反应能力，拟准备把特警队员从一目标处快速运送到另一目标处．通过测角仪观测到观测站C在目标A南偏西25°的方向上，B、D在A出发的一条南偏东35°走向的公路上（如图），测得C、B相距31千米，D、B相距20千米，C、D相距21千米，求A、D之间的距离．
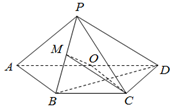1．如图，在四棱锥P-ABCD中，底面ABCD为梯形，AD∥BC，AB=BC=CD=1，DA=2，DP⊥平面ABP，O，M分别是AD，PB的中点．
（Ⅰ）求证：PD∥平面OCM；
（Ⅱ）若AP与平面PBD所成的角为60°，求线段PB的长．
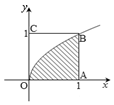2．如图，在正方形OABC内任取一点，取到函数$y=\sqrt{x}$的图象与x轴正半轴之间
（阴影部分）的点的概率等于$\frac{2}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网