题目内容
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的实轴长为4,截直线y=x-2所得弦长为20$\sqrt{2}$.求:(1)双曲线的方程;
(2)渐近线方程.
分析 (1)由直线与双曲线联立得(b2-4)x2+16x-16-4b2=0,利用截直线y=x-2所得弦长为20$\sqrt{2}$,即可求出双曲线的方程;
(2)利用双曲线方程,求出渐近线方程.
解答 解:(1)∵2a=4,∴a=2,
由直线与双曲线联立得(b2-4)x2+16x-16-4b2=0,
∴|x1-x2|=$\frac{4{b}^{2}}{|4-{b}^{2}|}$,
又弦长为$\sqrt{2}$|x1-x2|=20$\sqrt{2}$,∴|x1-x2|=20,
∴$\frac{4{b}^{2}}{|4-{b}^{2}|}$=20,解得b2=5或b2=$\frac{10}{3}$<4(舍去),
∴双曲线的方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1.
(2)∵双曲线的方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1,
∴渐近线方程为y=±$\frac{\sqrt{5}}{2}$x.
点评 本题考查双曲线的方程与性质,考查直线与双曲线位置关系的运用,属于中档题.

练习册系列答案
相关题目
3.计算机执行如图的程序,输出的结果是( )


| A. | 1,3 | B. | 4,9 | C. | 4,8 | D. | 4,12 |
5. 球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )
球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )
 球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )
球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )| A. | $\frac{4π}{3}$ | B. | 4π | C. | 12π | D. | 36π |
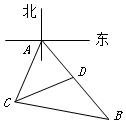 为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.
为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.