题目内容
16.已知直线l1:x-y-1=0,直线l2:x+y-3=0(I)求直线l1与直线l2的交点P的坐标;
(II)过点P的直线与x轴的非负半轴交于点A,与y轴交于点B,且S△AOB=4(O为坐标原点),求直线AB的斜率k.
分析 (1)联立直线得到方程组,求出交点坐标即可;(2)分别求出A、B的坐标,求出k的范围,关键三角形的面积求出k的值即可.
解答 解:(1)联立两条直线方程:
$\left\{\begin{array}{l}{x-y-1=0}\\{x+y-3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
所以直线l1与直线l2的交点P的坐标为(2,1);
(2)设直线方程为:y-1=k(x-2),
令x=0得y=1-2k,因此B(0,1-2k);
令y=0得x=2-$\frac{1}{k}$,因此$A(2-\frac{1}{k},0)$,
$\frac{2k-1}{k}≥0⇒k≥\frac{1}{2}ork<0$,
∴${S_{△AOB}}=|{\frac{1}{2}(1-2k)(2-\frac{1}{k})}|=4$,
解得k=-$\frac{1}{2}$或$k=\frac{3}{2}+\sqrt{2}$.
点评 本题考查了直线方程问题,考查直线的斜率,是一道基础题.

练习册系列答案
相关题目
3.计算机执行如图的程序,输出的结果是( )


| A. | 1,3 | B. | 4,9 | C. | 4,8 | D. | 4,12 |
8.已知数列{an}是等差数列,前n项和Sn,若S20>0,S21<0,那么Sn取得最大值时n=( )
| A. | 20 | B. | 21 | C. | 11 | D. | 10 |
5. 球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )
球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )
 球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )
球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )| A. | $\frac{4π}{3}$ | B. | 4π | C. | 12π | D. | 36π |
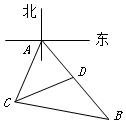 为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.
为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.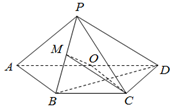 如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.