题目内容
3．已知空间两条不同的直线m、n和两个不同的平面α、β，则下列命题正确的是（ ）| A． | 若m∥α，n?α，则m∥n | B． | 若m∥α，n∥α，则m∥n | ||
| C． | 若m∥α，m?β，α∩β=n，则m∥n | D． | 若α∩β=m，m⊥n，则n⊥α |
分析 利用线面平行的判定与性质，即可得出结论．
解答 解：对于A，若m∥α，n?α，则m∥n或m，n异面，故不正确；
对于B，若m∥α，n∥αn∥α，则m，n相交或平行、异面，故B不正确；
对于C，根据线面平行的性质，可得正确；
对于D，利用线面垂直的判定，可得不正确．
故选：C．
点评 本题考查的知识点是空间直线与平面位置关系的判断，熟练掌握直线与平面之间位置关系的判定定理，性质定理，及定义和空间特征是解答此类问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．若480°角的终边上有一点（a，4），则a的值是（ ）
| A． | $\frac{4\sqrt{3}}{3}$ | B． | $-\frac{4\sqrt{3}}{3}$ | C． | 4$\sqrt{3}$ | D． | $-4\sqrt{3}$ |
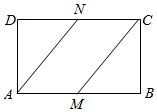如图在长方形ABCD中，$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b，N$是CD的中点，M是线段AB上的点，$|{\overrightarrow a}|=2，|{\overrightarrow b}|=1$．
13．
如图，四边形ABCD与ABEF均为矩形，BC=BE=2AB，二面角E-AB-C的大小为$\frac{π}{3}$．现将△ACD绕着AC旋转一周，则在旋转过程中，（ ）
如图，四边形ABCD与ABEF均为矩形，BC=BE=2AB，二面角E-AB-C的大小为$\frac{π}{3}$．现将△ACD绕着AC旋转一周，则在旋转过程中，（ ）| A． | 不存在某个位置，使得直线AD与BE所成的角为$\frac{π}{4}$ | |
| B． | 存在某个位置，使得直线AD与BE所成的角为$\frac{π}{2}$ | |
| C． | 不存在某个位置，使得直线AD与平面ABEF所成的角为$\frac{π}{4}$ | |
| D． | 存在某个位置，使得直线AD与平面ABEF所成的角为$\frac{π}{2}$ |