题目内容
2.计算:$\frac{tan68°+tan52°}{1-tan68°tan52°}$=$-\sqrt{3}$.分析 利用两角和的正切化简,再由诱导公式求值.
解答 解:$\frac{tan68°+tan52°}{1-tan68°tan52°}$=tan(68°+52°)=tan120°=tan(180°-60°)=-tan60°=$-\sqrt{3}$.
故答案为:$-\sqrt{3}$.
点评 本题考查两角和的正切,考查了三角函数的诱导公式,是基础题.

练习册系列答案
相关题目
10.已知数列{an}满足anan+1=2n,则$\frac{{a}_{7}}{{a}_{3}}$=( )
| A. | 2 | B. | 4 | C. | 5 | D. | $\frac{5}{2}$ |
3.已知空间两条不同的直线m、n和两个不同的平面α、β,则下列命题正确的是( )
| A. | 若m∥α,n?α,则m∥n | B. | 若m∥α,n∥α,则m∥n | ||
| C. | 若m∥α,m?β,α∩β=n,则m∥n | D. | 若α∩β=m,m⊥n,则n⊥α |
8.已知m,n是空间两条不重合的直线,α,β是两个不重合的平面,则下列命题中正确的是 ( )
| A. | m⊥α,α⊥β,m∥n⇒n∥β | B. | m⊥α,m⊥n,α∥β⇒n∥β | C. | m∥α,m⊥n,α∥β⇒n⊥β | D. | m⊥α,m∥n,α∥β⇒n⊥β |
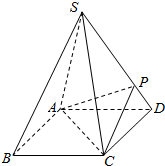 如图,正四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,CD=$\sqrt{2}$,点P在侧棱SD上,且SP=3PD.
如图,正四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,CD=$\sqrt{2}$,点P在侧棱SD上,且SP=3PD.