题目内容
15.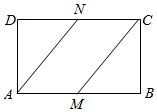 如图在长方形ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,N$是CD的中点,M是线段AB上的点,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$.
如图在长方形ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,N$是CD的中点,M是线段AB上的点,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$.(1)若M是AB的中点,求证:$\overrightarrow{AN}$与$\overrightarrow{CM}$共线;
(2)在线段AB上是否存在点M,使得$\overrightarrow{BD}$与$\overrightarrow{CM}$垂直?若不存在请说明理由,若存在请求出M点的位置;
(3)若动点P在长方形ABCD上运动,试求$\overrightarrow{AP}•\overrightarrow{AB}$的最大值及取得最大值时P点的位置.
分析 (1)建立如图所示平面直角坐标系,得到$\overrightarrow{AN}$与$\overrightarrow{CM}$的坐标,由共线向量基本定理得答案;
(2)假设存在M,设出M的坐标,由数量积运算求得M的坐标;
(3)直接利用向量在向量方向上的投影结合图形得答案.
解答 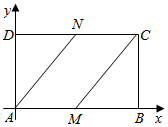 (1)证明:如图以AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系,
(1)证明:如图以AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系,
当M是AB的中点时,A(0,0),N(1,1),C(2,1),M(1,0),
$\overrightarrow{AN}=(1,1),\overrightarrow{CM}=(-1,-1)$,
由$\overrightarrow{AN}=-\overrightarrow{CM}$,可得$\overrightarrow{AN}$与$\overrightarrow{CM}$共线;
(2)解:假设线段AB上是否存在点M,使得$\overrightarrow{BD}$与$\overrightarrow{CM}$垂直,
设M(t,0)(0≤t≤2),则B(2,0),D(0,1),M(t,0),
$\overrightarrow{BD}=(-2,1),\overrightarrow{CM}=(t-2,-1)$,
由$\overrightarrow{BD}•\overrightarrow{CM}$=-2(t-2)-1=0,解得t=$\frac{3}{2}$,
∴线段AB上存在点$M(\frac{3}{2},0)$,使得$\overrightarrow{BD}$与$\overrightarrow{CM}$垂直;
(3)解:由图看出,当P在线段BC上时,$\overrightarrow{AP}$在$\overrightarrow{AB}$上的投影最大,
则$\overrightarrow{AP}•\overrightarrow{AB}$有最大值为4.
点评 本题考查平面向量的数量积运算,考查了向量在向量方向上的投影,体现了数形结合的解题思想方法,是中档题.

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案| A. | 2 | B. | 4 | C. | 5 | D. | $\frac{5}{2}$ |
| A. | 若m∥α,n?α,则m∥n | B. | 若m∥α,n∥α,则m∥n | ||
| C. | 若m∥α,m?β,α∩β=n,则m∥n | D. | 若α∩β=m,m⊥n,则n⊥α |
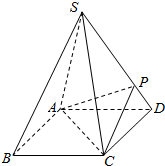 如图,正四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,CD=$\sqrt{2}$,点P在侧棱SD上,且SP=3PD.
如图,正四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,CD=$\sqrt{2}$,点P在侧棱SD上,且SP=3PD. 已知正方体AC1的棱长为a,过B1作B1E⊥BD1于点E,过点E作EF⊥BD于F.
已知正方体AC1的棱长为a,过B1作B1E⊥BD1于点E,过点E作EF⊥BD于F.