题目内容
设f(x)=x2+ax+b(a,b∈R),当x∈[-1,1]时,|f(x)|的最大值为m,则m的最小值为( )
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点:二次函数的性质
专题:函数的性质及应用,不等式的解法及应用
分析:若x∈[-1,1]时,|f(x)|的最大值为m,则4m≥|f(-1)|+|f(1)|+2|f(0)|≥2,解得m的最小值.
解答:
解:∵f(x)=x2+ax+b(a,b∈R),
当x∈[-1,1]时,|f(x)|的最大值为m,
∴4m≥|f(-1)|+|f(1)|+2|f(0)|=|1+A+B|+|1-A+B|+2|B|≥|(1+A+B)+(1-A+B)-2B|=2
m≥
,
即m的最小值为
,
故选:A
当x∈[-1,1]时,|f(x)|的最大值为m,
∴4m≥|f(-1)|+|f(1)|+2|f(0)|=|1+A+B|+|1-A+B|+2|B|≥|(1+A+B)+(1-A+B)-2B|=2
m≥
| 1 |
| 2 |
即m的最小值为
| 1 |
| 2 |
故选:A
点评:本题考查的知识点最值问题,二次函数的图象和性质,其中根据已知得到4m≥|f(-1)|+|f(1)|+2|f(0)|是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
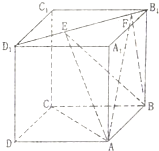 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
| ||
| 2 |
①AC⊥BE;
②平面AEF与平面ABCD的交线平行于直线EF;
③异面直线AE,BF所成的角为定值;
④三棱锥A-BEF的体积为定值,其中错误结论的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
从装有n+1个球的口袋中取出m个球(0<m≤n,m,n∈N),共有C
种取法.在这C
种取法中,可以分成一个指定的球被取到和未被取到两类:一类是该指定的球未被取到,共有C
•C
种取法;另一类是该指定的球被取到,共有C
•C
种取法.显然C10•Cnm+C11•Cnm-1=C
,即有等式:C
+C
=C
成立.试根据上述思想,则有:Cnm+Ck1•Cnm-1+Ck2•Cnm-2+…+Ckk•Cnm-k(其中当1≤k<m≤n,k,m,n∈N)为( )
m n+1 |
m n+1 |
0 1 |
m n |
1 1 |
m-1 n |
m n+1 |
m n |
m-1 n |
m n+1 |
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
函数f(x)=
x2-lnx的单调递减区间为( )
| 1 |
| 2 |
| A、(-1,1) |
| B、(0,1] |
| C、[1,+∞) |
| D、(-∞,-1)∪(0,1] |
观察下列各图,并阅读图形下面的文字,像这样,10条直线相交,交点的个数最多是( )


| A、40 | B、45 | C、50 | D、55 |
若抛物线y2=2px的焦点与椭圆
+
=1的右焦点重合,则p的值为( )
| x2 |
| 8 |
| y2 |
| 4 |
| A、-2 | B、2 | C、-4 | D、4 |
下面多面体中有12条棱的是( )
| A、四棱柱 | B、四棱锥 |
| C、五棱锥 | D、五棱柱 |
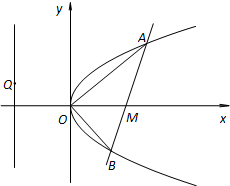 已知直线l过点M(4,0)且与抛物线y2=2px(p>0)交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
已知直线l过点M(4,0)且与抛物线y2=2px(p>0)交于A、B两点,以弦AB为直径的圆恒过坐标原点O.