题目内容
13.分别写有数字1,2,3,4的4张卡片,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为偶数的概率是$\frac{1}{3}$.分析 列举从这4张卡片中随机抽取2张情况总数,及满足取出的2张卡片上的数字之和为偶数情况数,代入古典概率概率计算公式,可得答案.
解答 解:从这4张卡片中随机抽取2张,共有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)6种抽法,
其中取出的2张卡片上的数字之和为偶数为(1,3),(2,4)共2种,
故取出的2张卡片上的数字之和为偶数的概率是$\frac{2}{6}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$
点评 本题主要考查了古典概率的计算公式在实际问题中的应用,解决问题的关键是要把基本事件的个数及指定的事件的个数分别求出.

练习册系列答案
相关题目
3.函数y=2x+log2(x+1)在区间[0,1]上的最大值和最小值之和为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.将函数y=sin2x的图象向左$\frac{π}{6}$平移个单位,向上平移1个单位,得到的函数解析式为( )
| A. | y=sin(2x+$\frac{π}{3}$)+1 | B. | y=sin(2x-$\frac{π}{3}$)+1 | C. | y=sin(2x+$\frac{π}{6}$)+1 | D. | y=sin(2x-$\frac{π}{6}$)+1 |
5.如图是函数f(x)=sin(x+φ)一个周期内的图象,则φ可能等于( )
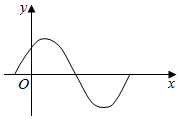

| A. | $\frac{5π}{6}$ | B. | $\frac{π}{2}$ | C. | $-\frac{π}{6}$ | D. | $\frac{π}{6}$ |
2.若质点A按规律s=2t2运动,则质点A在t=1时的瞬时速度是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{4}$ | D. | 4 |
3.由曲线y=x3,直线x=0,x=1及y=0所围成的曲边梯形的面积为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |