题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{cos(x-\frac{π}{2}),x∈[0,π]}\\{lo{g}_{2017}\frac{x}{π},x∈(π,+∞)}\end{array}\right.$,若有三个不同的实数a,b,c,使得f(a)=f(b)=f(c),则a+b+c的取值范围为( )| A. | (2π,2017π) | B. | (2π,2018π) | C. | ($\frac{3π}{2}$,$\frac{4035π}{2}$) | D. | (π,2017π) |
分析 作出y=f(x)的函数图象,根据函数的对称性可得a+b=π,求出c的范围即可得出答案.
解答 解:当x∈[0,π]时,f(x)=cos(x-$\frac{π}{2}$)=sinx,
∴f(x)在[0,π]上关于x=$\frac{π}{2}$对称,且fmax(x)=1,
又当x∈(π,+∞)时,f(x)=log2017$\frac{x}{π}$是增函数,
作出y=f(x)的函数图象如图所示: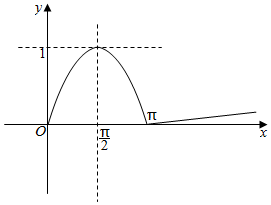
令log2017$\frac{x}{π}$=1得x=2017π,
∵f(a)=f(b)=f(c),
∴a+b=π,c∈(π,2017π),
∴a+b+c=π+c∈(2π,2018π).
故选:B.
点评 本题考查了函数零点与函数图象的关系,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
16.先把函数y=sin(x+φ)的图象上个点的横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),再向右平移$\frac{π}{3}$个单位,所得函数关于y轴对称,则φ的值可以是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $-\frac{π}{6}$ | D. | $-\frac{π}{3}$ |
3.如图所示的程序框图,若f(x)=logax,g(x)=lnx,输入x=2016,则输出的h(x)=( )
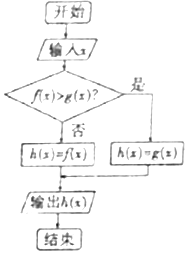

| A. | 2016 | B. | 2017 | C. | loga2016 | D. | loga2017 |
4.已知数列{an}满足an+1=an+$\frac{1}{2}$,则数列{an}是( )
| A. | 递增数列 | B. | 递减数列 | C. | 摆动数列 | D. | 常数列 |