题目内容
4．已知数列{an}满足an+1=an+$\frac{1}{2}$，则数列{an}是（ ）| A． | 递增数列 | B． | 递减数列 | C． | 摆动数列 | D． | 常数列 |
分析 利用数列的递推关系式，判断数列的性质，推出结果即可．
解答 解：数列{an}满足an+1=an+$\frac{1}{2}$，
可得an+1-an=$\frac{1}{2}$，可得数列是等差数列，公差为：$\frac{1}{2}＞0$，
所以数列是递增数列，
故选：A．
点评 本题考查数列的递推关系式的应用，等差数列的性质，是基础题．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
5．已知函数f（x）=$\left\{\begin{array}{l}{cos（x-\frac{π}{2}），x∈[0，π]}\\{lo{g}_{2017}\frac{x}{π}，x∈（π，+∞）}\end{array}\right.$，若有三个不同的实数a，b，c，使得f（a）=f（b）=f（c），则a+b+c的取值范围为（ ）
| A． | （2π，2017π） | B． | （2π，2018π） | C． | （$\frac{3π}{2}$，$\frac{4035π}{2}$） | D． | （π，2017π） |
15．若函数f（x）=（a-1）x3+ax2为奇函数，则f（1）=（ ）
| A． | 1 | B． | -1 | C． | -2 | D． | 0 |
12．已知ω＞0，函数$f（x）=sin（{ωx-\frac{π}{3}}）$在$（{\frac{π}{3}，\frac{π}{2}}）$上单调递减，则ω的取值范围是（ ）
| A． | $[{\frac{5}{2}，\frac{11}{3}}]$ | B． | $[{\frac{1}{2}，\frac{3}{4}}]$ | C． | $（{0，\frac{1}{2}}]$ | D． | $（{0，\frac{11}{3}}]$ |
19．已知函数$f（x）=-\frac{1}{3}{x^3}+m{x^2}+n（m，n，x∈R）$图象上任意两点A（x1，y1）、B（x2，y2）（x1＞x2），满足$f（{x_1}）-f（{x_2}）＜{x_1}-{x_2}+{x_1}^2-{x_2}^2$，则实数m的取值范围是（ ）
| A． | [0，2] | B． | （-∞，0） | C． | （0，2） | D． | [2，+∞] |
9．已知平面向量$\overrightarrow a$=（0，-1），$\overrightarrow b$=（1，1），|λ$\overrightarrow a$+$\overrightarrow b$|=$\sqrt{5}$，则λ的值为（ ）
| A． | 3 | B． | 2 | C． | 3或-1 | D． | 2或-1 |
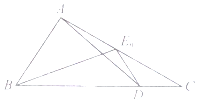如图，已知点D为△ABC的边BC上一点，$\overrightarrow{BC}=3\overrightarrow{DC}$，${E_n}（n∈{N^*}）$为边AC上的一列点，满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-（3{a_n}+2）•\overrightarrow{{E_n}D}$，其中实数列{an}中，an＞0，a1=1，则a5=（ ）
14．若满足∠A=30°，BC=10的△ABC恰好有不同的两个，则边AB长的取值范围为（ ）
| A． | （5，10） | B． | （10，20） | C． | [20，+∞） | D． | （5，10）∪[20，+∞） |