如图所示的程序框图.若f(x)=logax.g(x)=lnx.输入x=2016.则输出的hA．2016B．2017C．loga2016D．loga2017 题目和参考答案——青夏教育精英家教网——

题目内容

3．如图所示的程序框图，若f（x）=log_ax，g（x）=lnx，输入x=2016，则输出的h（x）=（　　）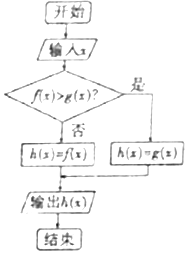

A．

2016

B．

2017

C．

log_a2016

D．

log_a2017

分析根据程序框图求出h（x）的解析式即可．

解答解：x=2016时，f（x）=log_a2016＜g（x）=ln2016，
故h（x）=f（x），
故选：C．

点评本题考查了程序框图，考查对数函数的性质，是一道基础题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

4．若曲线f（x）=$\sqrt{x}$在点（a，f（a））处的切线与两坐标轴围成的图形的面积为$\frac{1}{4}$，则a的值为1．

5．已知函数f（x）=$\left\{\begin{array}{l}{cos（x-\frac{π}{2}），x∈[0，π]}\\{lo{g}_{2017}\frac{x}{π}，x∈（π，+∞）}\end{array}\right.$，若有三个不同的实数a，b，c，使得f（a）=f（b）=f（c），则a+b+c的取值范围为（　　）

（2π，2017π）

（2π，2018π）

（$\frac{3π}{2}$，$\frac{4035π}{2}$）

（π，2017π）

11．已知函数f（x）=ln（2x+a）-e^2x-1．
（1）若函数f（x）在x=$\frac{1}{2}$处取得极值，求f（x）的单调区间；
（2）当a≤1时，f（x）＜0，求x的取值范围．

18．已知数列{a_n}满足a_n+1+2=$\frac{3{a}_{n}+4}{2{a}_{n}+3}$，且a₁=1，设b_n=$\frac{{a}_{n}+1}{{2}_{\;}}$，则数列{b_n•b_n+1}的前50项和为$\frac{50}{201}$．

8．定义在R上的函数f（x），恒有f（-x）+f（x）=0，且对任意x₁，x₂∈R有（x₁-x₂）[f（x₁）-f（x₂）]＜0成立．若对t∈[0，2]均有f（2t²-4）+f（4m-2t）≥f（0）成立，求m的取值范围．

15．若函数f（x）=（a-1）x³+ax²为奇函数，则f（1）=（　　）

12．已知ω＞0，函数$f（x）=sin（{ωx-\frac{π}{3}}）$在$（{\frac{π}{3}，\frac{π}{2}}）$上单调递减，则ω的取值范围是（　　）

$[{\frac{5}{2}，\frac{11}{3}}]$

$[{\frac{1}{2}，\frac{3}{4}}]$

$（{0，\frac{1}{2}}]$

$（{0，\frac{11}{3}}]$

13．命题：“?x＜-1，x²≥1”的否定是?x＜-1，x²＜1．