题目内容
10.已知函数f(x)=$\left\{{\begin{array}{l}{|lnx|,(0<x≤e)}\\{2-lnx,(x>e)}\end{array}}$,若a,b,c互不相等,且f(a)=f(b)=f(c),求a+b+c的取值范围.分析 根据f(x)的函数图象判断a,b,c的范围,利用f(a)=f(b)=f(c)得出a,b,c的关系,得出a+b+c关于a的函数,求出此函数的值域即可.
解答 解:作出函数f(x)的大致图象,如图所示: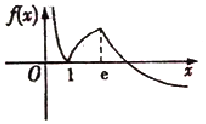
不妨设a<b<c,则0<a<1,1<b<e.
∵f(a)=f(b),即-lna=lnb,∴ab=1,即b=$\frac{1}{a}$,
同理-lna=2-lnc,∴$\frac{c}{a}$=e2,即c=ae2.
∴a+b+c=a+$\frac{1}{a}$+ae2=(e2+1)a+$\frac{1}{a}$,
又0<a<1,1<b<e,b=$\frac{1}{a}$,∴$\frac{1}{e}$<a<1,
令函数g(a)=(e2+1)a+$\frac{1}{a}$($\frac{1}{e}$<a<1),则g′(a)=e2+1-$\frac{1}{{a}^{2}}$>0,
∴g(a)在($\frac{1}{e}$,1)上单调递增,
∴g($\frac{1}{e}$)<g(a)<g(1),即2e+$\frac{1}{e}$<g(a)<e2+2.
∴2e+$\frac{1}{e}$<a+b+c<e2+2.
点评 本题考查了方程解与函数图象的关系,函数值域的计算,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.如图,已知向量$\overrightarrow a,\overrightarrow b,\overrightarrow c$,那么下列结论正确的是( )
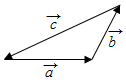

| A. | $\overrightarrow a+\overrightarrow b=\overrightarrow c$ | B. | $\overrightarrow a+\overrightarrow b=-\overrightarrow c$ | C. | $\overrightarrow a-\overrightarrow b=-\overrightarrow c$ | D. | $\overrightarrow b+\overrightarrow c=\overrightarrow a$ |
5.设x∈R,则“|x-1|<1”是“x2-x-2<0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
2.某舞步每一节共九步,且每一步各不相同,其中动作A三步,动作B三步,动作C三步,同一种动作相邻,则这种舞步一节中共有多少种不同的变化( )
| A. | 1296种 | B. | 216种 | C. | 864种 | D. | 1080种 |
2.某城市随机抽取一年内100天的空气质量指数(AQI)的监测数据,结果统计如表:
(1)若空气质量为严重污染则企业必须放假,试估计一年中(以360天计算)企业因为空气严重污染放假的天数;
(2)已知某企业每天的经济损失y(单位:元)与空气质量指数x的关系式为
y=$\left\{\begin{array}{l}{0,0≤x≤100}\\{4x-400,100<x≤300}\\{2000,x>300}\end{array}\right.$
1)若在本年内随机抽取一天,试估计这一天的经济损失超过400元的概率;
2)若以区间中点值计算空气质量指数,试估计一年中(以360天计算)企业因空气污染原因造成的经济损失是多少元.
| AQI | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数 | 6 | 14 | 18 | 27 | 20 | 15 |
(2)已知某企业每天的经济损失y(单位:元)与空气质量指数x的关系式为
y=$\left\{\begin{array}{l}{0,0≤x≤100}\\{4x-400,100<x≤300}\\{2000,x>300}\end{array}\right.$
1)若在本年内随机抽取一天,试估计这一天的经济损失超过400元的概率;
2)若以区间中点值计算空气质量指数,试估计一年中(以360天计算)企业因空气污染原因造成的经济损失是多少元.
3.观察数组:(-1,1,-1),(1,2,2),(3,4,12),(5,8,40),…,(an,bn,cn),则cn的值不可能为( )
| A. | 112 | B. | 278 | C. | 704 | D. | 1664 |