题目内容
3.观察数组:(-1,1,-1),(1,2,2),(3,4,12),(5,8,40),…,(an,bn,cn),则cn的值不可能为( )| A. | 112 | B. | 278 | C. | 704 | D. | 1664 |
分析 由题意an=-1+(n-1)×2=2n-3,bn=2n-1,从而得到cn=anbn=(2n-3)•2n-1,由此能求出结果.
解答 解:由题意an=-1+(n-1)×2=2n-3,bn=2n-1,
cn=anbn=(2n-3)•2n-1,
在A中,当n=5时,c5=(2×5-3)×24=112,成立;
在B中,当n=6时,c6=(2×6-3)•25=288>277,故B不成立;
在C中,当n=7时c7=(2×7-3)•26=704,成立;
在D中,当n=8时,${c}_{8}=(2×8-3)•{2}^{7}$=1664,成立.
故选:B.
点评 本题考查数列中的元素的判断,考查进行简单的合情推理,考查学生分析解决问题的能力,考查数列的性质及应用,是中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
8.某四棱锥的三视图如图所示,该四棱锥外接球的体积为( )


| A. | $\frac{{\sqrt{6}}}{3}π$ | B. | $\frac{{\sqrt{6}}}{2}π$ | C. | $\sqrt{6}π$ | D. | $3\sqrt{6}π$ |
15.某个几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 24+π | B. | 24+2π | C. | 20+π | D. | 20+2π |
12.在如图所示的算法流程图中,输出S的值为( )
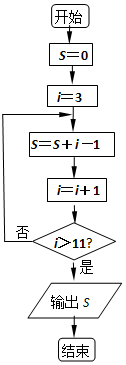

| A. | 51 | B. | 52 | C. | 53 | D. | 54 |
13.过点A(2,3)的直线的参数方程为$\left\{\begin{array}{l}{x=2+t}\\{y=3+2t}\end{array}\right.$(t为参数),若此直线与直线x-y+3=0相交于点B,则|AB|=( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | $\frac{3\sqrt{5}}{2}$ |
