题目内容
1．如图，已知向量$\overrightarrow a，\overrightarrow b，\overrightarrow c$，那么下列结论正确的是（ ）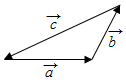
| A． | $\overrightarrow a+\overrightarrow b=\overrightarrow c$ | B． | $\overrightarrow a+\overrightarrow b=-\overrightarrow c$ | C． | $\overrightarrow a-\overrightarrow b=-\overrightarrow c$ | D． | $\overrightarrow b+\overrightarrow c=\overrightarrow a$ |
分析 根据向量的三角形法则即可得到
解答 解：如图，已知向量$\overrightarrow a，\overrightarrow b，\overrightarrow c$，根据向量的三角形法则可得，$\overrightarrow{a}$+$\overrightarrow{b}$=-$\overrightarrow{c}$，
故选：B
点评 本题考查了向量的三角形法则，属于基础题
练习册系列答案
全优点练单元计划系列答案
相关题目
12．边长为2的正三角形ABC内（包括三边）有点P，$\overrightarrow{PB}$$•\overrightarrow{PC}$=1，则$\overrightarrow{AP}$•$\overrightarrow{AB}$的范围是（ ）
| A． | [2，4] | B． | [$\frac{3-\sqrt{5}}{2}$，4] | C． | [3-$\sqrt{5}$，2] | D． | [$\frac{3-\sqrt{5}}{2}$，3-$\sqrt{5}$] |
9．已知曲线y=axcosx在$（{\frac{π}{2}，0}）$处的切线的斜率为$\frac{1}{2}$，则实数a的值为（ ）
| A． | $\frac{π}{2}$ | B． | -$\frac{π}{2}$ | C． | $\frac{1}{π}$ | D． | $-\frac{1}{π}$ |
16．设函数f（x）=2kx3+4（k-1）x2-3k2-2在区间（0，2）上是减函数，则k的取值范围是（ ）
| A． | $k＜\frac{2}{5}$ | B． | $k≤\frac{2}{5}$ | C． | $0＜k≤\frac{2}{5}$ | D． | $0≤k≤\frac{2}{5}$ |
13．正弦函数是奇函数，因为f（x）=sin（x+1）是正弦函数，所以f（x）=sin（x+1）是奇函数．以上推理（ ）
| A． | 结论正确 | B． | 大前提错误 | C． | 小前提错误 | D． | 以上都不对 |