题目内容
1.已知直线l1:x+ay=2a+2和l2:ax+y=a+1.(Ⅰ) 若l1⊥l2,求a的值;
(Ⅱ) 若l1∥l2,求这两条平行线间的距离.
分析 (Ⅰ)当两条直线垂直时,A1A2+B1B2=0,解方程求出a的值.
(Ⅱ)利用两直线平行时,由A1B2+A2B1=0且A1C2+A2C1≠0,求出a的值,再根据平行线间的距离公式即可求出.
解答 解:(Ⅰ)已知直线直线l1:x+ay=2a+2,和l2:ax+y=a+1,
若l1⊥l2,由A1A2+B1B2=0得:a+a=0,
∴a=0.
(Ⅱ)解法一:若l1∥l2,由A1B2+A2B1=0且A1C2+A2C1≠0,得$\left\{\begin{array}{l}{1-{a}^{2}=0}\\{-a(a+1)+2a+2≠0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a=±1}\\{a≠-1且a≠2}\end{array}\right.$,a=1.
这时,l1:x+-4=0和l2:x+y-2=0,
这两条平行线间的距离$d=\frac{{|{C_1}-{C_2}|}}{{\sqrt{{A^2}+{B^2}}}}=\frac{2}{{\sqrt{2}}}=\sqrt{2}$.
点评 本题考查两直线相交、垂直、平行、重合的条件,体现了转化的数学思想.属于基础题.

练习册系列答案
相关题目
12.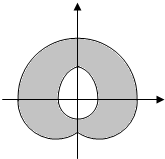 如图是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}中的点在平面上运动时留下的阴影,中间形如“水滴”部分的平面面积为( )
如图是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}中的点在平面上运动时留下的阴影,中间形如“水滴”部分的平面面积为( )
 如图是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}中的点在平面上运动时留下的阴影,中间形如“水滴”部分的平面面积为( )
如图是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}中的点在平面上运动时留下的阴影,中间形如“水滴”部分的平面面积为( )| A. | $\frac{11}{6}π-\sqrt{3}$ | B. | $\frac{7}{3}π-\sqrt{3}$ | C. | $π+\sqrt{3}$ | D. | π+2 |
11.直线l1:3mx+8y+3m-10=0过定点( )
| A. | (-1,-$\frac{4}{5}$) | B. | (-1,$\frac{4}{5}$) | C. | (-1,$\frac{5}{4}$) | D. | (-1,-$\frac{5}{4}$) |