��Ŀ����
3����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���У�F1��F2Ϊ���ҽ��㣬��F1��F2Ϊֱ����Բ����Բ�ڵ�һ�������Ľ���ֱ�ΪA��B����ֱ��AB��ֱ��x+$\sqrt{3}$y-7=0���ഹֱ������Բ��������Ϊ��������| A�� | $\frac{\sqrt{3}+1}{2}$ | B�� | $\frac{\sqrt{3}-1}{2}$ | C�� | $\sqrt{3}$-1 | D�� | $\frac{\sqrt{5}-1}{2}$ |
���� �������ֱ��AB��б��Ϊ$\sqrt{3}$������б��Ϊ$\frac{��}{3}$�����ݶԳ��Կ�֪$��AO{F}_{2}=\frac{��}{3}$��$��A{F}_{2}{F}_{1}=\frac{��}{6}$
��Rt��AF1F2�У�$A{F}_{1}=\sqrt{3}c��A{F}_{2}=c$����$\sqrt{3}c+c=2a$��⇒$\frac{c}{a}=\frac{2}{\sqrt{3}+1}=\sqrt{3}-1$��
��� �⣺��ͼ��ʾ����ֱ��AB��ֱ��x+$\sqrt{3}$y-7=0���ഹֱ����ֱ��AB��б��Ϊ$\sqrt{3}$������б��Ϊ$\frac{��}{3}$��
���ݶԳ��Կ�֪$��AO{F}_{2}=\frac{��}{3}$��$��A{F}_{2}{F}_{1}=\frac{��}{6}$
��Rt��AF1F2��$A{F}_{1}=\sqrt{3}c��A{F}_{2}=c$��
������Բ�Ķ�����$\sqrt{3}c+c=2a$��⇒$\frac{c}{a}=\frac{2}{\sqrt{3}+1}=\sqrt{3}-1$��
��ѡC��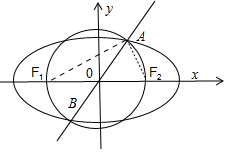
���� ���⿼������Բ�������ʣ�����Ĺؼ���Ҫ����������Բ��Բ�����ʣ�ֱ�ߵ�λ�ù�ϵ�������е��⣮

��ϰ��ϵ�д�
�����Ŀ
19����֪����A={x|1��2x��16}��B={x|x��a}����A��B=A����ʵ��a��ȡֵ��Χ�ǣ�������
| A�� | a��4 | B�� | a��4 | C�� | a��0 | D�� | a��0 |
17��Ϊ�˵õ�����y=cos2x��ͼ��ֻҪ�Ѻ���$y=sin��2x-\frac{��}{3}��$��ͼ�������еĵ㣨������
| A�� | ����ƽ���ƶ�$\frac{5��}{12}$����λ���� | B�� | ����ƽ���ƶ�$\frac{5��}{12}$����λ���� | ||
| C�� | ����ƽ���ƶ�$\frac{5��}{6}$����λ���� | D�� | ����ƽ���ƶ�$\frac{5��}{6}$����λ���� |
8��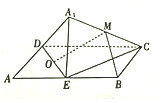 ��ͼ������ABCD�У�AB=2AD��EΪ��AB���е㣬����ADE��ֱ��DE��ת�ɡ�A1DE��A1∉ƽ��ABCD������M��O�ֱ�Ϊ�߶�A1C��DE���е㣬���ڡ�ADE��ת�����У�����˵��������ǣ�������
��ͼ������ABCD�У�AB=2AD��EΪ��AB���е㣬����ADE��ֱ��DE��ת�ɡ�A1DE��A1∉ƽ��ABCD������M��O�ֱ�Ϊ�߶�A1C��DE���е㣬���ڡ�ADE��ת�����У�����˵��������ǣ�������
 ��ͼ������ABCD�У�AB=2AD��EΪ��AB���е㣬����ADE��ֱ��DE��ת�ɡ�A1DE��A1∉ƽ��ABCD������M��O�ֱ�Ϊ�߶�A1C��DE���е㣬���ڡ�ADE��ת�����У�����˵��������ǣ�������
��ͼ������ABCD�У�AB=2AD��EΪ��AB���е㣬����ADE��ֱ��DE��ת�ɡ�A1DE��A1∉ƽ��ABCD������M��O�ֱ�Ϊ�߶�A1C��DE���е㣬���ڡ�ADE��ת�����У�����˵��������ǣ�������| A�� | ��ƽ��A1DE��ֱ��ֱ�߱���ֱ��BM��ֱ | |
| B�� | ��E��EG��BM��G��ƽ��A1DC�����A1EGΪ��ֵ | |
| C�� | һ������ij��λ�ã�ʹDE��MO | |
| D�� | ����A1-ADE�����뾶����AD�ij�֮��Ϊ��ֵ |
15���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����֪��B=30�㣬��ABC�����Ϊ$\frac{3}{2}$����sinA+sinC=2sinB����b��ֵΪ��������
| A�� | 4+2$\sqrt{3}$ | B�� | 4-2$\sqrt{3}$ | C�� | $\sqrt{3}$-1 | D�� | $\sqrt{3}$+1 |
13��2016��9��30���ܽ��ס��ر���ǿ������Ѳ���ݳ�����ɽ��ʡ�������ĺ�������������У�ij��У4000��Ů����6000�������а��ֲ������ȡ��50��ѧ���������ʾ����飬���鷢�ֹۿ��ݳ�����δ�ۿ��ݳ����������ͬ�����йۿ��ݳ����Ů��Ϊ15�ˣ�
��1�����ݵ������������2��2����������ͨ�������ж��Ƿ��ڷ�����ĸ��ʲ�����0.005��ǰ������Ϊ���ۿ��ݳ������Ա��йء���
��2���ӹۿ��ݳ����4��������3��Ů���г�ȡ���ˣ���ǡ�ó鵽һ��������һ��Ů���ĸ��ʣ�
�ο���ʽ��K2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$������n=a+b+c+d��
��1�����ݵ������������2��2����������ͨ�������ж��Ƿ��ڷ�����ĸ��ʲ�����0.005��ǰ������Ϊ���ۿ��ݳ������Ա��йء���
��2���ӹۿ��ݳ����4��������3��Ů���г�ȡ���ˣ���ǡ�ó鵽һ��������һ��Ů���ĸ��ʣ�
| �ۿ� | δ�ۿ� | �ϼ� | |
| �� | |||
| ���� | |||
| �ϼ� | 50 |
| P��K2��k0�� | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
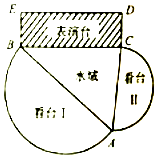 ��ˮ���Ͻ�һ�����չ㳡�����չ㳡�ɿ�̨��̨��������ˮ��ABC�������α���̨BCDE�ĸ����ֹ��ɣ���ͼ������̨��̨���Ƿֱ���AB��ACΪֱ����������Բ�������ҿ�̨�������ǿ�̨��������3�������α���̨BCDE �У�CD=10�ף�������ˮ��ABC�����Ϊ$400\sqrt{3}$ƽ���ף����BAC=�ȣ�
��ˮ���Ͻ�һ�����չ㳡�����չ㳡�ɿ�̨��̨��������ˮ��ABC�������α���̨BCDE�ĸ����ֹ��ɣ���ͼ������̨��̨���Ƿֱ���AB��ACΪֱ����������Բ�������ҿ�̨�������ǿ�̨��������3�������α���̨BCDE �У�CD=10�ף�������ˮ��ABC�����Ϊ$400\sqrt{3}$ƽ���ף����BAC=�ȣ�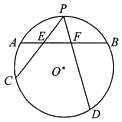 ��ͼ����֪ABΪԲO��һ���ң���PΪ��$\widehat{AB}$���е㣬����P����������PC��PD�ֱ�AB�ڵ�E��F
��ͼ����֪ABΪԲO��һ���ң���PΪ��$\widehat{AB}$���е㣬����P����������PC��PD�ֱ�AB�ڵ�E��F