题目内容
在极坐标系中，已知圆ρ=2cosθ与直线5ρcosθ+12ρsinθ+a=0相切，求实数a的值．
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把极坐标方程化为直角坐标方程，再根据圆心到直线的距离等于半径求得a的值．
解答：
解：圆ρ=2cosθ 即 （x-1）2+y2=1，表示以（1，0）为圆心、半径等于1的圆．
直线5ρcosθ+12ρsinθ+a=0 即 5x+12y+a=0，
根据圆心到直线的距离等于半径可得
=
=1，
求得a=8，或a=-18．
直线5ρcosθ+12ρsinθ+a=0 即 5x+12y+a=0，
根据圆心到直线的距离等于半径可得
| |5+0+a| | ||
|
| |5+a| |
| 13 |
求得a=8，或a=-18．
点评：本题主要考查把极坐标方程化为直角坐标方程的方法，点到直线的距离公式的应用，直线和圆的位置关系，属于基础题．
练习册系列答案
相关题目
已知O是△ABC内部一点，且3
+
+
=
，
•
=6，∠BAC=60°，则△OBC的面积为（ ）
| OA |
| OB |
| OC |
| 0 |
| AB |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将相邻的5个不同编号的房间安排给5个工作人员临时休息，假定每个人可以选择任一房间，且选择各个房间是等可能的，若恰有2个房间无人选择且这2个房间不相邻，则不同的安排方式的总数为（ ）
| A、60 | B、90 |
| C、150 | D、900 |
不等式组
，表示的平面区域为Ω，直线y=kx-1与区域Ω有公共点，则实数k的取值范围为（ ）
|
| A、（0，3] |
| B、[-1，1] |
| C、（-∞，3] |
| D、[3，+∞） |
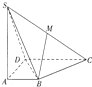四棱锥S-ABCD中，SA⊥平面ABCD，底面四边形ABCD为直角梯形，AB∥CD，AD⊥DC，SA=AD=DC=2，AB=1．