已知平面向量$\overrightarrow a.\overrightarrow b$.$\overrightarrow a=.\overrightarrow b=$.若$\overrightarrow a∥\overrightarrow b$.则实数k=( )A．2B．-2C．4D．-4 题目和参考答案——青夏教育精英家教网—

题目内容

12．已知平面向量$\overrightarrow a，\overrightarrow b$，$\overrightarrow a=（{-1，1}），\overrightarrow b=（{2，k}）$，若$\overrightarrow a∥\overrightarrow b$，则实数k=（　　）

A．

B．

-2

C．

D．

-4

分析利用向量共线定理即可得出．

解答解：∵$\overrightarrow a∥\overrightarrow b$，∴2+k=0，解得k=-2．
故选：B．

点评本题考查了向量共线定理，考查了推理能力与计算能力，属于基础题．

练习册系列答案

$\frac{3}{2}$+$\sqrt{2}$

$\frac{3}{2}$+2$\sqrt{2}$

3．数列{a_n}满足a_n+1=$\left\{\begin{array}{l}2{a_n}，0≤{a_n}≤\frac{1}{2}\\ 2{a_n}-1，\frac{1}{2}＜{a_n}＜1\end{array}$，a₁=$\frac{3}{5}$，S_n为{a_n}的前n项和，则S₂₀₁₆=1008．

20．设tanα，tanβ是方程x²+3x-2=0的两个根，则tan（α+β）的值为（　　）

7．

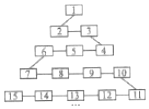一般吧数字出现的规律满足如图的模型称为蛇形模型：数字1出现在第1行，数字2，3出现在第2行；数字6，5，4（从左到右）出现在第3行；数字7，8，9，10出现在第4行，以此类推，第21行从左到右的第4个数字应是228．

17．已知向量$\overrightarrow m=（sinx，-1）$，向量$\overrightarrow n=（\sqrt{3}cosx，-\frac{1}{2}）$，函数$f（x）=（\overrightarrow m+\overrightarrow n）•\overrightarrow m$．
（1）求f（x）的解析式及单调增区间；
（2）已知a，b，c分别为△ABC内角A，B，C的对边，A为锐角，a=2$\sqrt{3}$，c=4，且f（A）恰是f（x）在$[{0，\frac{π}{2}}]$上的最大值，求A，b和△ABC的面积S．

4．已知函数f（x）=$\sqrt{2}sinωxcosωx+\sqrt{2}{cos^2}ωx-\frac{{\sqrt{2}}}{2}（{ω＞0}）$，若x=$\frac{π}{4}$是函数f（x）的一条对称轴，则实数ω的值可以是（　　）

1．已知集合A={x|0＜x＜2}，B={x|1-x²＞0}，则A∩（∁_RB）=（　　）

2．黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：

则第n个图案中的地面砖共有5n+2块．

试题分类