题目内容
12.若直线ax-by+2=0 (a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )| A. | $\frac{3}{2}$+$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{2}$+2$\sqrt{2}$ |
分析 先求出圆心和半径,由弦长公式求得圆心到直线ax-by+2=0的距离d=0,直线ax-by+2=0经过圆心,可得$\frac{1}{2}$a+b=1,代入式子再利用基本不等式可求式子的最小值.
解答 解:圆x2+y2+2x-4y+1=0 即 (x+1)2+(y-2)2=4,圆心为(-1,2),半径为2,
设圆心到直线ax-by+2=0的距离等于d,则由弦长公式得2$\sqrt{4-{d}^{2}}$=4,
解得d=0,即
直线ax-by+2=0经过圆心,
∴-a-2b+2=0,
∴$\frac{1}{2}$a+b=1,
∴($\frac{1}{a}$+$\frac{1}{b}$)($\frac{1}{2}$a+b)=$\frac{1}{2}$+1+$\frac{b}{a}$+$\frac{a}{2b}$≥$\frac{3}{2}$+2$\sqrt{\frac{b}{a}•\frac{a}{2b}}$=$\frac{3}{2}$+$\sqrt{2}$,当且仅当a=$\sqrt{2}$b时等号成立,
故式子的最小值为$\frac{3}{2}$+$\sqrt{2}$,
故选:A
点评 本题考查直线和圆的位置关系,弦长公式以及基本不等式的应用,属于中档题

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
2.某品牌电动汽车的耗电量y与速度x之间满足的关系式为y=$\frac{1}{3}$x3-$\frac{39}{2}$x2-40x(x>0),为使耗电量最小,则速度为( )
| A. | 30 | B. | 40 | C. | 50 | D. | 60 |
3.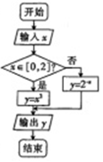 如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
 如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )| A. | [-3,-2] | B. | [-3,-2)∪{2} | C. | [-3,2] | D. | [-3,-2]∪{2} |
20.设函数$f(x)=\left\{\begin{array}{l}2{e^{x-1}},x<2\\{log_3}({{x^2}-1}),x≥2\end{array}\right.$,则f(f(2))的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
7.在平面直角坐标系xOy中,已知双曲线C1:2x2-y2=1,过C1的左顶点引C1的一条渐进线的平行线,则该直线与另一条渐进线及x轴围成的三角形的面积( )
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{2}}}{16}$ |
17.抛物线y2=4x的焦点到双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线的距离是$\frac{\sqrt{3}}{2}$,则双曲线的虚轴长是( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 6 |